expressão trigonométrica

Resolva a equação trigonométrica:



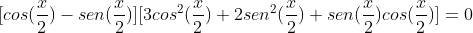
refiz e refiz essa expressão e não consegui reduzi-la a nada, no primeiro momento pensei que fosse possível reduzi-la em um quadrado perfeito, mas nem pelas formulas do arco metade ou transformando em produto consegui fazer, alguém pra ajudar?

Cara, não é para reduzir essa expressão.

Olha, primeiramente, vou maquiar o problema para me facilitar.

cos(x/2) = m
sen(x/2) = n


[m-n].[3m²+2n²+mn]=0

Ou seja:

m-n=0   (I)            ou       3m²+2n²+mn=0  (II)


(I)   m-n=0
      cos(x/2) - sen (x/2)=0
      cos(x/2) = sen(x/2)
      cos²(x/2) = sen²(x/2)
      cos²(x/2) = 1 - cos²(x/2)
      2cos²(x/2) = 1
      cos(x/2) =+/- √2/2
      
Portanto:          cos(x/2) = cos( ∏/4)  *
                            x/2= ∏/4
                             x= ∏/2 rad

*OBS: x= ∏/2  pois se eu admitir outros valores para os quais o cosseno possua o mesmo valor a conta: cos(x/2)-sen(x/2) não dará 0


(II) 3m² + 2n² + mn = 0
     3m² + nm + 2n² = 0

 ∆  = n² -24n²
 ∆ = -23n²

 ∆  < 0 , a equação não possui raízes reais



Solução:

S= {x= ∏/2 +2k∏, c/ k ∈ ℤ }

OBS2: Eu não sei se na segunda condição não há mesmo raízes reais, eu tentei fazer de outro jeito, porém eu caí em uma equação de terceiro grau (eu ainda não sei resolver essas equações  hihi)

é que eu imaginei ter de reduzir pra chegar no resultado, eu não tinha visto essa de substituir, muito obrigado.

eu desenvolvi assim:
3m² + 2n² + mn = 0, mas m=n
3m² + 2m² m*m = 0

3m² + 2m² + m² = 0
6m² = 0 ---> m=0


cos(x/2) = 0
cos(x/2) = cos(∏/2)
x/2 = ∏/2
x = ∏ + 2k∏, com c/ k ∈ ℤ 


S = {x= ∏/2 +2k∏, c/ k ∈ ℤ  ou  x = ∏ + 2k∏, com c/ k ∈ ℤ }, agr completa.




como você chegou a uma equação do terceiro grau?

Man, essa segunda relação não está correta.

m≠n 

(m=n é algo particular da primeira equação. As duas são independentes, você precisa calcular o valor para que uma dê zero e depois para a outra.)
Se você duvidar, basta substituir x/2 por 90º(180º/2), você verá que na segunda equação dará 2.

A equação que eu cheguei foi:

y³+y+4=0  (na verdade antes era de 6º grau)

sendo y=cos²(x/2)

só substituir sen²x=1-cos²x  na segunda equação (OBS: dá um trabalho danado fazer isso).

de alguma forma não podemos pensar que essas duas equações do enunciado era uma única, e a expressão nos apresentou como ela seria fatorada?
vou refazê-la, obrigado pela ajuda.

A solução do Gabriel está correta. Há necessidade apenas de uma complementação:

(m - n).(3m² + 2n²+ mn = 0) ---> Existem duas possibilidades:

1) m - n = 0 --> m = n ---> cos(x/2) = sen(x/2) ---> Existem duas possibilidades para isto acontecer, na 1ª volta:

1.1) Ângulo no 1º quadrante ---> x/2 = pi/4 ---> x = pi/2
1.2) Ângulo no 3º quadrante ---> x/2 = 5.pi/4 ---> x = 5.pi/2 ---> x = 2pi + pi/2 ---> x = pi/2

2) 3m² + 2.m²+ mn = 0 ---> 3m² + nm + 2n² = 0 ---> ∆ = - 25n² ---> Não há raízes reais

obrigado pela ajuda, esclareci minhas dúvidas agora.