(Uefs 2015.2) Questão difícil
5 participantes
Página 2 de 2
Página 2 de 2 •  1, 2
1, 2
 (Uefs 2015.2) Questão difícil
(Uefs 2015.2) Questão difícil
Relembrando a primeira mensagem :

Se as coordenadas dos pontos P1 = (x1, y1) e P2 = (x2, y2) satisfazem o sistema de
equações
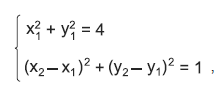 ,
,
então P2 pode ser qualquer ponto da região, representada na figura, cuja área é
A) 3π u.a.
B) 4π u.a.
C) 5π u.a.
D) 8π u.a. < resposta
E) 9π u.a.

Se as coordenadas dos pontos P1 = (x1, y1) e P2 = (x2, y2) satisfazem o sistema de
equações
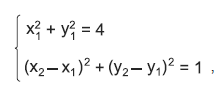 ,
,então P2 pode ser qualquer ponto da região, representada na figura, cuja área é
A) 3π u.a.
B) 4π u.a.
C) 5π u.a.
D) 8π u.a. < resposta
E) 9π u.a.
Laislilas- Jedi

- Mensagens : 435
Data de inscrição : 28/03/2014
Idade : 29
Localização : Salvador,Bahia,Brasil
 Re: (Uefs 2015.2) Questão difícil
Re: (Uefs 2015.2) Questão difícil
Esta questão não é difícil, ao contrário, é muito fácil e imediata.
O sistema de equações
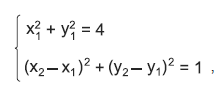
Explicitamente, nos diz:
1) O quadrado da distância entre P1 e (0; 0) é 4, logo, distam 2 e
2) O quadrado da distância entre eles é 1, logo, distam 1.
(1) nos diz que, em R², o L.G. de P1 é circunferência de raio 2 centrada em (0; 0)
(2) nos diz que há, em R², uma circunferência centrada em P1, de raio 1, que é o L.G. de P2.
Podemos satisfazer essas afirmações, em R², com um conjunto representado pela região sombreada da figura, uma coroa circular de raios r=2-1 e R=2+1, figura resultante da rotação completa ( 360º) de um P1 qualquer, levando consigo o L.G. de P2 (circunferência de raio 2 centrada em P1):

A = (R² - r²) ∏ = (9 - 1) ∏
A = 8 ∏ u.a. --> D
O sistema de equações
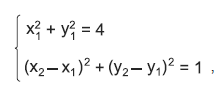
Explicitamente, nos diz:
1) O quadrado da distância entre P1 e (0; 0) é 4, logo, distam 2 e
2) O quadrado da distância entre eles é 1, logo, distam 1.
(1) nos diz que, em R², o L.G. de P1 é circunferência de raio 2 centrada em (0; 0)
(2) nos diz que há, em R², uma circunferência centrada em P1, de raio 1, que é o L.G. de P2.
Podemos satisfazer essas afirmações, em R², com um conjunto representado pela região sombreada da figura, uma coroa circular de raios r=2-1 e R=2+1, figura resultante da rotação completa ( 360º) de um P1 qualquer, levando consigo o L.G. de P2 (circunferência de raio 2 centrada em P1):
A = (R² - r²) ∏ = (9 - 1) ∏
A = 8 ∏ u.a. --> D
rihan- Estrela Dourada

- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
 Re: (Uefs 2015.2) Questão difícil
Re: (Uefs 2015.2) Questão difícil
Acredito que a dificuldade estava em enxergar que a 2ª equação tratava-se de uma equação reduzida da circunferência de raio=1 e centro em P1. Obrigado!
EsdrasCFOPM- Estrela Dourada

- Mensagens : 1247
Data de inscrição : 22/02/2016
Idade : 30
Localização : Salvador, Bahia, Brasil
 Re: (Uefs 2015.2) Questão difícil
Re: (Uefs 2015.2) Questão difícil
EsdrasCFOPM escreveu:Acredito que a dificuldade estava em enxergar que a 2ª equação tratava-se de uma equação reduzida da circunferência de raio=1 e centro em P1. Obrigado!
A segunda equação nos diz que o quadrado da distância entre 2 pontos é 1...
O conjunto de pontos que satisfaz essa afirmação (Lugar Geométrico, L.G.) em R² é uma circunferência.
Você, se não souber o básico, vai ter dificuldade em tudo.
TEM que saber de cor, para não perder TEMPO nos concursos:
1 ) Equações da reta
2 ) Equações da parábola
3 ) Equações da circunferência
4 ) Equações da elipse
5 ) Distância entre dois pontos
6 ) Distância entre ponto e reta
7 ) Distância entre ponto e plano
8 ) Área do triângulo (ou paralelogramo) dados 3 pontos
9 ) Áreas e volumes de figuras planas e sólidos mais comuns
Etc.
Ou estudar Álgebra Vetorial, e deduzir, na hora, as fórmulas, perdendo algum tempo.
Para ficar fácil a questão é necessário e suficiente ESTUDAR :study: e, na hora do exame LER, RELER, :study: LER DE NOVO :bounce: , ANALISAR, PENSAR, SINTETIZAR :scratch: , e, fazer tudo isso, dentro do menor tempo possível
rihan- Estrela Dourada

- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
 Re: (Uefs 2015.2) Questão difícil
Re: (Uefs 2015.2) Questão difícil
É realmente um caminho difícil mas se fosse fácil não se chamaria desafio e nem teria graça. hehehe
Obrigado pelas dicas!
Obrigado pelas dicas!
EsdrasCFOPM- Estrela Dourada

- Mensagens : 1247
Data de inscrição : 22/02/2016
Idade : 30
Localização : Salvador, Bahia, Brasil
 Re: (Uefs 2015.2) Questão difícil
Re: (Uefs 2015.2) Questão difícil
Agora, da maneira complicada e difícil, que nem eu nem Medeiros gostamos... :evil:
1) Dados:
vetor A(a; b)
vetor B(x; y)
a² + b² = 4
|B - A|² = 1
2) Sabendo-se:
B - A = (x - a; y - b)
ângulo entre A e B = β
|A|² = a² + b²
|B|² = x² + y²
|B - A|² = (x - a)² + (y - b)² = |B|² + |A|² - 2|A||B|cosβ
A.B = |A||B| cosβ = ax + by
3) Tem-se:
a) (a e b) e (x e y) não podem ser nulos simultaneamente.
b) x² + y² + a² + b² - 2V(a² + b² ) V(x² + y²)cosβ = 1
x² + y² + 4 - 2( 2 V(x² + y²)cosβ = 1
x² + y² + 4 - 4 cosβ V(x² + y²) = 1
cosβ = (x² + y² + 3) /4V(x² + y²)
cos²β = (x² + y² + 3)² / 16(x² + y²)
Então:
0 <= (x² + y² + 3)² / 16(x² + y²) <= 1
c) (x - a)² + (y - b)² = 1
x² + y² + a² + b² - 2(ax + by ) = 1
x² + y² + 4 - 2(ax + by) = 1
x² + y² + 3 = 2(ax + by)
x² + y² = 2(ax + by) - 3
x² + y² > 0
Então:
ax + by > 3/2
ax + by = A.B
|A||B|cosβ > 3/2
4|B|cosβ > 3/2
cosβ > 3/(8|B|)
cos²β > 9/(64(x² + y²))
Então:
Então:
9/(64(x² + y²)) < (x² + y² + 3)² / 16(x² + y²) <= 1
9 < 4(x² + y² + 3)² <= 64(x² + y²)
9 < 4(x² + y² + 3)² / (x² + y²) <= 64
9/4 < (x² + y² + 3)² / (x² + y²) <= 16
Mandando pro Wolfram ... :twisted: Alguém tem que trabalhar nesse fórum...

E fosse em R³ ?
Dava uma coroa (casca) esférica ou um toro (toroide) :face:
 ????
????
1) Dados:
vetor A(a; b)
vetor B(x; y)
a² + b² = 4
|B - A|² = 1
2) Sabendo-se:
B - A = (x - a; y - b)
ângulo entre A e B = β
|A|² = a² + b²
|B|² = x² + y²
|B - A|² = (x - a)² + (y - b)² = |B|² + |A|² - 2|A||B|cosβ
A.B = |A||B| cosβ = ax + by
3) Tem-se:
a) (a e b) e (x e y) não podem ser nulos simultaneamente.
b) x² + y² + a² + b² - 2V(a² + b² ) V(x² + y²)cosβ = 1
x² + y² + 4 - 2( 2 V(x² + y²)cosβ = 1
x² + y² + 4 - 4 cosβ V(x² + y²) = 1
cosβ = (x² + y² + 3) /4V(x² + y²)
cos²β = (x² + y² + 3)² / 16(x² + y²)
Então:
0 <= (x² + y² + 3)² / 16(x² + y²) <= 1
c) (x - a)² + (y - b)² = 1
x² + y² + a² + b² - 2(ax + by ) = 1
x² + y² + 4 - 2(ax + by) = 1
x² + y² + 3 = 2(ax + by)
x² + y² = 2(ax + by) - 3
x² + y² > 0
Então:
ax + by > 3/2
ax + by = A.B
|A||B|cosβ > 3/2
4|B|cosβ > 3/2
cosβ > 3/(8|B|)
cos²β > 9/(64(x² + y²))
Então:
Então:
9/(64(x² + y²)) < (x² + y² + 3)² / 16(x² + y²) <= 1
9 < 4(x² + y² + 3)² <= 64(x² + y²)
9 < 4(x² + y² + 3)² / (x² + y²) <= 64
9/4 < (x² + y² + 3)² / (x² + y²) <= 16
Mandando pro Wolfram ... :twisted: Alguém tem que trabalhar nesse fórum...
E fosse em R³ ?
Dava uma coroa (casca) esférica ou um toro (toroide) :face:

rihan- Estrela Dourada

- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
Página 2 de 2 •  1, 2
1, 2
 Tópicos semelhantes
Tópicos semelhantes» UEFS(2015.2) Questão 52
» (UEFS 15.2) PA -difícil
» uefs polinomios dificil
» (UEFS) DIFÍCIL - Lei de diluição de Ostwald
» (UEFS 15.2) Difícil - Números complexos
» (UEFS 15.2) PA -difícil
» uefs polinomios dificil
» (UEFS) DIFÍCIL - Lei de diluição de Ostwald
» (UEFS 15.2) Difícil - Números complexos
Página 2 de 2
Permissões neste sub-fórum
Não podes responder a tópicos












