[Resolvido]Valor de a (número complexo)

Se o número complexo z = 1 + i é uma das raízes da equação 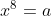, o valor de a é:

gabarito: 16.


Bom, eu queria uma ajudinha pois minha resposta não tá batendo :/ Eu fiz assim:

z = 1 + i -----> |z| = \/2 ----> sen = \/2/2 .:. cos = \/2/2 ---> â = 45° = pi/4

> x^8 = a

Z0 = \/2 (cis pi/4) = 1 + i Z4 = \/2 (cis 5.pi/4) = -1 - i
Z1 = \/2 (cis pi/2) = i Z5 = \/2 (cis 3.pi/2) = -i
Z2 = \/2 (cis 3.pi/2) = -1 + i Z6 = \/2 (cis 7.pi/4) = 1 - i
Z3 = \/2 (cis pi) = -1 Z7 = \/2 (cis 2.pi) = 1

x^8 = a
a = [(1+ii)i].[(-1+i)-1].[(-1-i)-i].[(1-i)1] = (i-1)(1-i)(i-1)(1-i) = (i-1)^2 (1-i)^2 = -4

Alguém pode me dizer se minha resolução tá errada?

Sim Carol, está errada pois esqueceu de um detalhe:



Você se esqueceu de elevar o módulo também, mas corrigindo isso poderia ter feito como demonstrou.

Carol

Como o Douglas mostrou, existem várias maneiras de calcular.
Vou mostrar outra:

(1 + i)^8 = [(1 + i)²]^4 = (2i)^4 = (2^4)*(i^4) = 16*1 = 16

ah, ok! Obrigada, gente!