(Coréia)parábola e circunferência

por kill* Ter 14 Jul 2015, 16:19

Seja D o domínio
l (x,y) l x ≥0 , y ≥0 l

Um circulo contido em D toca uma parábola y=x²/2 no ponto (2,2) e também toca o eixo x. calcule o raio do circulo.

gab:

por **VictorCoe** Sáb 22 Ago 2015, 23:16

I) Tendo uma noção de derivadas, temos que a reta tangente a parábola no ponto (2,2) é:

*) Achando o coeficiente angular:

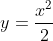
$y=\frac{x^2}{2}$

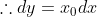
$\therefore dy=x_0dx$

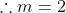
$\therefore m=2$

**) Achando o linear, temos que no ponto (2,2)

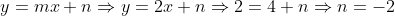
$y=mx + n \Rightarrow y=2x+n \Rightarrow 2 = 4+n \Rightarrow n= -2$

Logo, a equação da reta é :

$y=2x-2$

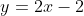
II)
(Coréia)parábola e circunferência 317cyf5

(Coréia)parábola e circunferência 317cyf5

Temos que se a reta é tangente a parabola no ponto (2,2), ela também é tangente a circunferência. Pelo teorema do bico, o segmento pontilhado cortará o ângulo que constitui o coeficiente a angular da reta tangente em dois. Portanto, temos que a tangente do ângulo/2 será:

$tg\alpha = \frac{2tg\left ( \frac{\alpha }{2} \right )}{1-tg^2\left ( \frac{\alpha }{2} \right )}$

$\Rightarrow 2 = \frac{2tg\left ( \frac{\alpha }{2} \right )}{1-tg^2\left ( \frac{\alpha }{2} \right )}$

$\therefore tg\left ( \frac{\alpha }{2} \right )=\frac{\sqrt{5}-1}{2}$

III) Temos que o raio da circunferência é R=Dtg(a/2) sendo que D é a distância do ponto (1,0) ao (2,2), logo:

$R=tg\left ( \frac{\alpha }{2} \right )\sqrt{(2-1)^2+2^2}$

$R=tg\left ( \frac{\alpha }{2} \right )\sqrt{5}$

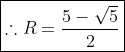
$\boxed{\therefore R=\frac{5-\sqrt{5}}{2}}$

(Coréia)parábola e circunferência

(Coréia)parábola e circunferência

Re: (Coréia)parábola e circunferência

Um fórum livre e democrático.