(Escola Naval) Função real.
2 participantes
Página 1 de 1
 (Escola Naval) Função real.
(Escola Naval) Função real.
Sabendo-se que f é uma função real de variável real, tal que a derivada segunda de f em x é  e que
e que 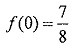 e
e  , o valor de f(π) é
, o valor de f(π) é

Gabarito: D
 e que
e que 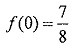 e
e  , o valor de f(π) é
, o valor de f(π) é
Gabarito: D
RamonLucas- Estrela Dourada

- Mensagens : 2034
Data de inscrição : 26/03/2015
Idade : 31
Localização : Brasil, Búzios.
 Re: (Escola Naval) Função real.
Re: (Escola Naval) Função real.
Integre a segunda derivada para achar a primeira função derivada :
=&space;\int&space;cos^2x+1)
=&space;\int&space;\frac{cos2x&space;+1}{2}&space;+1)
=&space;\int&space;\frac{cos2x&space;+3}{2}dx)
Isso vai dar
f'(x) = (6x + sen (2x))/4 + C
Fazendo f'(0) = 2:
2 = 0 + C --> C = 2
Então f'(x) = (6x + sen (2x))/4 + 2
O que nos resta é integrarmos novamente para acharmos f(x)
f (x) =∫ 3x/2 dx + ∫sen (2x)/4 dx + ∫2 dx
f (x) = 3x^2/4 - cos (2x)/8 + 2x + C'
Fazendo f (0) :
f (0) = 0 - 1/8 + 0 + C' = 7/8 --> C' = 1
Logo substituindo C' e fazendo f (pi) :
f (pi) = 3pi^2/4 - cos (2pi)/8 + 2pi + 1
Portanto,
f (pi) = 3pi^2/4 + 2pi + 7/8
Item D
Isso vai dar
f'(x) = (6x + sen (2x))/4 + C
Fazendo f'(0) = 2:
2 = 0 + C --> C = 2
Então f'(x) = (6x + sen (2x))/4 + 2
O que nos resta é integrarmos novamente para acharmos f(x)
f (x) =∫ 3x/2 dx + ∫sen (2x)/4 dx + ∫2 dx
f (x) = 3x^2/4 - cos (2x)/8 + 2x + C'
Fazendo f (0) :
f (0) = 0 - 1/8 + 0 + C' = 7/8 --> C' = 1
Logo substituindo C' e fazendo f (pi) :
f (pi) = 3pi^2/4 - cos (2pi)/8 + 2pi + 1
Portanto,
f (pi) = 3pi^2/4 + 2pi + 7/8
Item D

VictorCoe- Fera

- Mensagens : 530
Data de inscrição : 20/02/2012
Idade : 27
Localização : Fortaleza/Ceará
 Tópicos semelhantes
Tópicos semelhantes» (Escola Naval) O domínio da função real.
» (Escola Naval - 2004)Função real| Derivável.
» (Escola Naval - 2004) Função real derivável.
» escola naval(função)
» (Escola Naval) Função com log.
» (Escola Naval - 2004)Função real| Derivável.
» (Escola Naval - 2004) Função real derivável.
» escola naval(função)
» (Escola Naval) Função com log.
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












