Seja C a circunferência de centro (2, 0) e ra

Seja C a circunferência de centro (2, 0) e raio 2, e considere O e P os pontos de interseção de C com o eixo Ox. Sejam T e S pontos de C que pertencem, respectivamente, às retas r e s, que se interceptam no ponto M, de forma que os triângulos OMT e PMS sejam congruentes, como mostra a figura a seguir. 



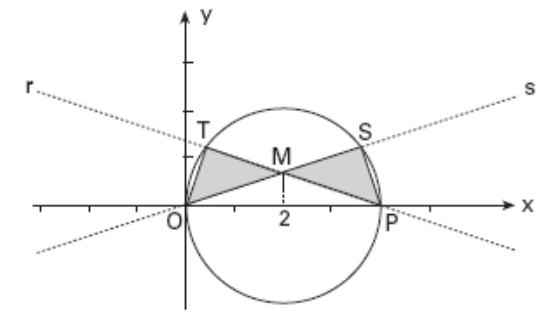
a) Dê a equação de C e, sabendo que a equação de s é, y = 3/x determine as coordenadas de S. 
b) Calcule as áreas do triângulo OMP e da região sombreada formada pela união dos triângulos OMT e PMS

Olá, 

A equação de (s) é y =3/x ou y = x/3 ?


Obrigado.

Me perdoe Mestre Jose Carlos, a equação s é y=x/3

- equação da circunferência:

( x - 2 )² + ( y - 0 )² = 4

x² - 4x + 4 + y² = 4

x² + y² - 4x = 0


- equação da reta (s):

y = ( 1/3 )x


- coordenadas do ponto M:

M pertence a reta (s) -> x = 2 > y = 2/3 -> M( 2, 2/3 )


- coordenadas do ponto O:

O( 0, 0 )


- coordenadas do ponto S:

S pertence à reta (s) -> S( xS, xS/3 )


- interseção da reta (s) com circunferêcia:

x² - 4x + ( x²/9 ) = 0

10x² - 36x = 0

x = 0 -> descartada

ou x = 36/10 -> x = 18/5

y = ( 1/3 )*( 18/5 ) = 18/15 = 6/5

S( 18/5 , 6/5 )


- reta (r) que passa pelos pontos ( 4, 0 ) e M( 2, 2/3 ):

( y - 0 )/(2/3 ) = ( x - 4 )/( - 2 )

y = ( - 1/3 )x + ( 4/3 )


- interseção de (r) com circunferência:


x² - 4x + ( ( 4/3 ) - ( x/3 ) ) = 0

raízes: x = 2/5 ou x = 4 ( descartar)

x = 2/3 -> y = 6/5

T( 2/5 , 6/5 )


- área do triângulo formado pelos pontos ( 0, 0 ) , ( 4, 0 ) e ( 2, 2/3 ):


S = 4*(2/3)/2 = 8/6 = 4/3 



- área do triângulo OMT:

.................| 0 ........ 0 ........ 1 |
S = ( 1/2 )* | 2/5......6/5........1 | | = ( 1/2 )*| [ 0 + 0 + ( 4/15 ) - ( 12/5 ) = ( 1/2 )*| ( - 32/15 ) | = 16/15
.................| 2 .........2/3 ......1 |


- área do triângulo MPS é igual a área do triângulo OMT:

S = 16/5


- área da região sombreada:

S = 2*( 16/5 ) = 32/3


* confira cálculos *