SISTEMAS 3

por José Fernandes de Brito Ter 26 maio 2015, 22:19

Assinale a alternativa que expressa a solução e a classificação do sistema de equações lineares, a seguir:
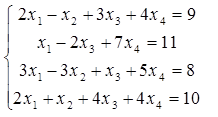
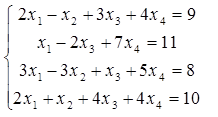
SISTEMAS 3 Sistemas%201

	S={(-1,0,1,2)} Classificação: Sistema possível e determinado
	S={ } Classificação: Sistema impossível
	S={(-1,0,1,2)} Classificação: Sistema possível e indeterminado
	S={(-1,0,-1,2)} Classificação: Sistema possível e determinado
	S={(-1,0,t,2)} Classificação: Sistema possível e indeterminado

por iResolva Qui 28 maio 2015, 17:27

Olá José Fernandes

Num sistema de equações lineares, podemos alterar a ordem das equações que continuaremos obtendo a mesma resposta. Assim, o sistema dado pode ser reestruturado do seguinte modo:

x1 - 2x3 + 7x4 = 11
2x1 - x2 + 3x3 + 4x4 = 9
3x1 - 3x2 + x3 + 5x4 = 8
2x1 + x2 + 4x3 + 4x4 = 10

Escalonando esse sistema, chegamos a um sistema linear equivalente (admite as mesmas soluções):

x1 - 2x3 + 7x4 = 11 (EQUAÇÃO I)
-x2 + 7x3 - 10x4 = -13 (EQUAÇÃO II)
x3 - x4 = -1 (EQUAÇÃO III)
-x4 = -2 (EQUAÇÃO IV)

Da equação IV, obtemos x4 = 2

Substituindo na Equação III:
x3 - (2) = -1. Logo x3 = 1

Fazendo o mesmo na Equação II, com os valores já encontrados:
-x2 + 7(1) - 10(2) = -13. Resolvendo, chegamos a x2 = 0

E, por último, substituindo os valores encontrados na Equação I:
x1 - 2(1) + 7(2) = 11, temos que x1 = -1.

Portanto, o sistema linear dado no exercício possui uma única solução, ou seja, ele é Possível e Determinado, e a solução é

S = {-1, 0, 1, 2}

Logo, a alternativa correta é a primeira

Abraços!