Inequação do 2º grau
5 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Inequação do 2º grau
por laurorio Ter 28 Abr 2015, 13:03
Qual é a condição suficiente para que a expressão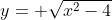 
represente uma função?
laurorio- Matador
- Mensagens : 1320
Data de inscrição : 22/03/2015
Idade : 26
Localização : Rio de Janeiro - Brasil
Re: Inequação do 2º grau
por Carlos Adir Ter 28 Abr 2015, 13:10
Uma função é necessário que para um valor de x, exista somente um valor de y.
Temos que y=√(x²-4) é uma função, mas y²=x²-4 não é mais uma função. Pois se pegamos x=4, então y=2 raiz de 3 ou y=-2 raiz de 3.
=\sqrt{x^2-4} "f(x)=\sqrt{x^2-4}")
é uma função, cujo domínio é
=\left]-\infty&space;,&space;\&space;-2&space;\right]\cup&space;\left[2,&space;\&space;+\infty&space;\right&space;[ "D(f)=\left]-\infty , \ -2 \right]\cup \left[2, \ +\infty \right [")
Temos que y=√(x²-4) é uma função, mas y²=x²-4 não é mais uma função. Pois se pegamos x=4, então y=2 raiz de 3 ou y=-2 raiz de 3.
é uma função, cujo domínio é
____________________________________________
← → ↛ 
⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ º ª ⁿ ⁱ
₀ ₁ ₂ ₃ ₄ ₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ₐ ₑ ₒ ₓ ₔ
∴ ≈ ≠ ≡ ≢ ≤ ≥ × ± ∓ ∑ ∏ √ ∛ ∜ ∝ ∞
∀ ∃ ∈ ∉ ⊂ ⊄ ⋂ ⋃ ∧ ∨ ℝ ℕ ℚ ℤ ℂ
⊥ ║ ∡ ∠ ∢ ⊿ △ □ ▭ ◊ ○ ∆ ◦ ⊙ ⊗ ◈
Αα Ββ Γγ Δδ Εε Ζζ Ηη Θθ Ιι Κκ Λλ Μμ Νν Ξξ Οο Ππ Ρρ Σσς Ττ Υυ Φφ Χχ Ψψ Ωω ϑ ϒ ϖ ƒ ij ℓ
∫ ∬ ∭ ∳ ∂ ∇
ℛ ℜ ℰ ℳ ℊ ℒ
Carlos Adir- Monitor
- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
Re: Inequação do 2º grau
por Elcioschin Ter 28 Abr 2015, 14:38
Complementando
x² - 4 >= 0 ---> x² >= 4 ---> x =< -2 ou x >= 2
x² - 4 >= 0 ---> x² >= 4 ---> x =< -2 ou x >= 2
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Inequação do 2º grau
por catherine Ter 03 Abr 2018, 12:41
Boa tarde,
poderiam refazer a questão, novamente? Apesar das duas explicações não consegui assimilar muita coisa...
Obrigada!
poderiam refazer a questão, novamente? Apesar das duas explicações não consegui assimilar muita coisa...
Obrigada!
catherine- Iniciante
- Mensagens : 23
Data de inscrição : 17/08/2017
Idade : 26
Localização : São Carlos, São paulo, Brasil
Re: Inequação do 2º grau
por Elcioschin Ter 03 Abr 2018, 13:07
Para existir uma função ela deve ser real
Para ser real o radicando não pode ser nulo ---> x² - 4 ≥ 0
Para ser real o radicando não pode ser nulo ---> x² - 4 ≥ 0
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
catherine gosta desta mensagem
Re: Inequação do 2º grau
por mvrs_04 Dom 26 Nov 2023, 23:01
Creio que não possa ser negativoElcioschin escreveu:Para existir uma função ela deve ser real
Para ser real o radicando não pode ser nulo ---> x² - 4 ≥ 0
mvrs_04- Iniciante
- Mensagens : 4
Data de inscrição : 28/09/2023
Re: Inequação do 2º grau
por Elcioschin Seg 27 Nov 2023, 09:40
Certamente o radicando não pode ser negativo!
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
catherine e mvrs_04 gostam desta mensagem
Tópicos semelhantes» inequacao 2 grau
» Inequação de 2º grau
» Inequação do 2º grau
» Inequação do 1° grau
» Inequação do 2º grau
» Inequação de 2º grau
» Inequação do 2º grau
» Inequação do 1° grau
» Inequação do 2º grau
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
