Inequação
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Inequação
Inequação
Para que a equação (1 - a²)x² + 2ax - 1 = 0 tenha raízes pertencente ao intervalo ]0 ; 1[, é necessário e suficiente que a > 2. Prove.
Obrigada!
Obrigada!
Convidado- Convidado
 Re: Inequação
Re: Inequação
Seja f(x) = (1-a²)x²+2ax-1, então temos que:
f(0) = (1-a²).0² + 2a . 0 - 1 ---> f(0)=-1
f(1) = (1-a²).1² + 2a . 1 - 1 ---> f(1) = -a²+2a-1+1 = 1-(a-1)²
Como é necessário que existam duas raizes entre 0 e 1, então é necessário que f(1)<0.
Portanto:
^2&space;<&space;0&space;\Rightarrow&space;(a-1)^2&space;>&space;1&space;\Rightarrow&space;|a-1|&space;>&space;1&space;\Rightarrow&space;\begin{cases}a<0&space;\\&space;a>2&space;\end{cases})
Mas veja que para tal fato ocorrer é necessário que o vértice da parábola seja maior que 0, então:
}<1&space;\\&space;0&space;<&space;\dfrac{4(-1)(1-a^2)-(2a)^2}{4&space;(1-a^2)}&space;\end{cases}&space;\Rightarrow&space;\begin{cases}&space;0&space;<&space;\dfrac{a}{a^2-1}<1&space;\\&space;0<&space;\dfrac{1}{a-1}\end{cases})
Ou seja, é necessário que satisfaça as três condições ao mesmo tempo:
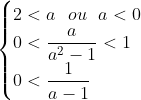
E concluimos que isto vem quando:
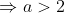
f(0) = (1-a²).0² + 2a . 0 - 1 ---> f(0)=-1
f(1) = (1-a²).1² + 2a . 1 - 1 ---> f(1) = -a²+2a-1+1 = 1-(a-1)²
Como é necessário que existam duas raizes entre 0 e 1, então é necessário que f(1)<0.
Portanto:
Mas veja que para tal fato ocorrer é necessário que o vértice da parábola seja maior que 0, então:
Ou seja, é necessário que satisfaça as três condições ao mesmo tempo:
E concluimos que isto vem quando:
____________________________________________
← → ↛  ⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥
 ⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ º ª ⁿ ⁱ
₀ ₁ ₂ ₃ ₄ ₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ₐ ₑ ₒ ₓ ₔ
∴ ≈ ≠ ≡ ≢ ≤ ≥ × ± ∓ ∑ ∏ √ ∛ ∜ ∝ ∞
∀ ∃ ∈ ∉ ⊂ ⊄ ⋂ ⋃ ∧ ∨ ℝ ℕ ℚ ℤ ℂ
⊥ ║ ∡ ∠ ∢ ⊿ △ □ ▭ ◊ ○ ∆ ◦ ⊙ ⊗ ◈
Αα Ββ Γγ Δδ Εε Ζζ Ηη Θθ Ιι Κκ Λλ Μμ Νν Ξξ Οο Ππ Ρρ Σσς Ττ Υυ Φφ Χχ Ψψ Ωω ϑ ϒ ϖ ƒ ij ℓ
∫ ∬ ∭ ∳ ∂ ∇
 ℛ ℜ ℰ ℳ ℊ ℒ
ℛ ℜ ℰ ℳ ℊ ℒ
Carlos Adir- Monitor

- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
 Re: Inequação
Re: Inequação
Boa noite; trouxe 2 soluções alternativas, das quais acho que a segunda seja a melhor para esse problema.
Outra solução:
f(x) = (1 - a²)x² + 2ax - 1
(1-a²)*f(0) > 0 ---> 0 não está entre as raízes, portanto ou as duas são positivas ou as duas são negativas.
0 < a/(a²-1) < 1 ---> vértice da parábola entre 0 e 1; assim, a maior das raízes será obrigatoriamente positiva, mas como colocamos que o 0 não está entre as raízes, a outra também obrigatoriamente será.
(1-a²)*[(1-a²)1² + 2a - 1] > 0 ----> 1 não está entre as raízes; assim, ou ambas estão entre 0 e 1 ou ambas são maiores que 1; mas como já colocamos que o vértice está entre 0 e 1, isso força com que a maior raiz tambem esteja no intervalo
Jutando as condições:
a²-1 > 0
0 < a/(a²-1) < 1
a(a²-1)(a - 2) > 0
Resolvendo você encontra exatamente a > 2.
Outro modo:
Resolvendo a equação para x:
x = (-a +- 1)/(1-a²)
Queremos que:
0 < (a+1)/(a²-1) < 1
0 < (a-1)/(a²-1) < 1
0 < 1/(a-1) < 1
0 < 1/(a+1) < 1
Resolvendo o simples intervalo acima, temos que a > 2.
Outra solução:
f(x) = (1 - a²)x² + 2ax - 1
(1-a²)*f(0) > 0 ---> 0 não está entre as raízes, portanto ou as duas são positivas ou as duas são negativas.
0 < a/(a²-1) < 1 ---> vértice da parábola entre 0 e 1; assim, a maior das raízes será obrigatoriamente positiva, mas como colocamos que o 0 não está entre as raízes, a outra também obrigatoriamente será.
(1-a²)*[(1-a²)1² + 2a - 1] > 0 ----> 1 não está entre as raízes; assim, ou ambas estão entre 0 e 1 ou ambas são maiores que 1; mas como já colocamos que o vértice está entre 0 e 1, isso força com que a maior raiz tambem esteja no intervalo
Jutando as condições:
a²-1 > 0
0 < a/(a²-1) < 1
a(a²-1)(a - 2) > 0
Resolvendo você encontra exatamente a > 2.
Outro modo:
Resolvendo a equação para x:
x = (-a +- 1)/(1-a²)
Queremos que:
0 < (a+1)/(a²-1) < 1
0 < (a-1)/(a²-1) < 1
0 < 1/(a-1) < 1
0 < 1/(a+1) < 1
Resolvendo o simples intervalo acima, temos que a > 2.

Ashitaka- Monitor

- Mensagens : 4365
Data de inscrição : 12/03/2013
Localização : São Paulo
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












