Equações logarítmicas

por Danilo Vilela Qua 01 Set 2010, 09:32

Gostaria de ajuda na seguinte questão:

Sabe-se que os gráficos das funções reais definidas por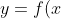 $y=f(x)=2^{x+1}-k$ e $y=g(x)=log_{3}(x+3^{2k-1})$ se cortam em um ponto P do eixo das ordenadas. Obtenha o valor da constante K e o ponto P.

por **Jose Carlos** Qua 01 Set 2010, 11:52

f(x) = [2^(x+1)] - k

g(x) = log...[x+(3^(2k-1)) ]
............3

ponto P do eixo das ordenadas: P(0, yP )

temos:

f(0) = (2^1) - k

g(0) = log...^[3^(2k-*1) ]
............3

sendo:

f(0) = g(0) -> 2-k = log...3^(2k-1)
...............................3

3^(2-k) = 3^(2k-1)

2-k = 2k-1

k = 1 -> P(0, 1)

por Danilo Vilela Qua 01 Set 2010, 14:24

No mesmo exercício ele faz a seguinte pergunta:

Qual a raiz (ou zero) da função g?

Fiz assim:

g(x) = 0
log x + 3^2k - 1 = 0
3

3^0 = x + 3^1
1 = x + 3
x = -2

Estou certo fazendo assim? Obrigado.