Derivação Implicita II

por L.Lawliet Dom 14 Dez 2014, 11:39

Determine a equação da reta tangente à elipse (x/a)²+(y/b)² = 1 no ponto (x_o;y_o), com y_o≠0

por Gabriel Rodrigues Ter 30 Dez 2014, 16:41

Observe que uma cônica pode ser vista como uma curva de nível de uma função de duas variáveis a valores reais. Nesse caso, temos a curva de nível da função 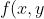$f(x,y) = \frac{x^2}{a^2} + \frac{y^2}{b^2}$ no nível c = 1.

Além disso, sabemos que o vetor gradiente de uma função, definida em R² e valores em R, é normal à sua curva de nível (desde que o ponto analisado pertença à curva de nível). Isto é, o vetor diretor da reta tangente procurada é normal ao gradiente da função, este calculado no ponto (x0, y0).
A partir disto, demonstra-se que a equação da reta tangente à curva de nível da função f, no ponto (xo,yo), é:

$\bigtriangledown f(x_0,y_0) \cdot \left[(x,y)-(x_0,y_0) \right ] = 0$

Calculemos o gradiente:

$\bigtriangledown f(x_0,y_0) = \left(\frac{\partial f}{\partial x}(x_0,y_0) , \frac{\partial f}{\partial y}(x_0,y_0) \right )$

$\Rightarrow \bigtriangledown f (x_0,y_0) = \left( \frac{2x_0}{a^2},\frac{2y_0}{b^2} \right)$

Resolvendo o produto escalar, ficamos com:

$\left(\frac{x_0}{a^2}\right)x + \left(\frac{y_0}{b^2}\right)y = \frac{x_0^2}{a^2} + \frac{y_0^2}{b^2} : y_0 \neq 0$

Como foi dito, tudo isso só é válido se o ponto (xo,yo) pertence à curva de nível. Isso implica que o lado direito da equação acima é igual a 1 (o nível é c=1). Ou seja, a equação fica da forma:

$\left(\frac{x_0}{a^2}\right)x + \left(\frac{y_0}{b^2}\right)y = 1 : y_0 \neq 0$

Derivação Implicita II

Derivação Implicita II

Re: Derivação Implicita II

Um fórum livre e democrático.