Equação do 2º grau
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Equação do 2º grau
por Darienzo Seg 06 Out 2014, 11:00
Determine m na equação do 2º g. (3m – 2)x² + 2mx + 3m = 0, para que tenha uma única raíz entre -1 e 0.
Darienzo- Iniciante
- Mensagens : 8
Data de inscrição : 17/09/2014
Idade : 73
Localização : cuiabá, Mato Grosso, Brasil.
Re: Equação do 2º grau
por Carlos Adir Seg 06 Out 2014, 12:00
Veja que é uma equação de segundo grau.
x^2+2mx+3m&space;=0 "(3m-2)x^2+2mx+3m =0")
Veja que se m>(2/3), teremos uma função crescente, e dado os valores:
(3m-2) > 0; (2m)>0, 3m >0
Assim, não teremos uma solução para m>(2/3)
E caso todos os valores forem negativos, então
(3m-2)<0, 2m<0, 3m<0
E então não teria solução também.
E não podemos admitir o valor de (2/3), pois a anularia a equação de segundo grau.
Assim:
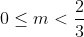
Veja que só tem um ponto de encontro, assim, o valor de Delta equivale a zero.
Portanto:
^2&space;-&space;4&space;\times&space;(3m-2)&space;\times&space;(3m)\\&space;4m^2-12m(3m-2)=0&space;\\&space;4m^2-36m^2+24m=0\\&space;32m^2-24m=0\\4m^2-3m&space;=&space;0\\&space;m(4m-3)=0\\&space;m_1=\dfrac{3}{4}&space;\leftrightarrow&space;m_2=0 "\\ \Delta = b^2 - 4ac \\ 0 = (2m)^2 - 4 \times (3m-2) \times (3m)\\ 4m^2-12m(3m-2)=0 \\ 4m^2-36m^2+24m=0\\ 32m^2-24m=0\\4m^2-3m = 0\\ m(4m-3)=0\\ m_1=\dfrac{3}{4} \leftrightarrow m_2=0")
Assim, m=0
Pra saber se cumpre, podemos descobrir o valor de x quando toca no ponto y=0
x^2+2mx+3m&space;=0\\x=\dfrac{-b&space;\pm&space;\sqrt{\Delta}}{2a}\\&space;x=\dfrac{-2m}{2(3m-2)}\\&space;x=\dfrac{m}{2-3m} "\\(3m-2)x^2+2mx+3m =0\\x=\dfrac{-b \pm \sqrt{\Delta}}{2a}\\ x=\dfrac{-2m}{2(3m-2)}\\ x=\dfrac{m}{2-3m}")
Se a solução está entre -1 e 0, então:
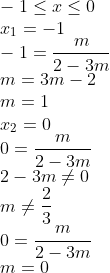
Portanto, m só pode ser 0. E então a equação fica com cara:
x^2&space;+&space;2(0)&space;x&space;+&space;3&space;(0)&space;=&space;0\\&space;-2x^2=0 "\\(3 \times 0 - 2)x^2 + 2(0) x + 3 (0) = 0\\ -2x^2=0")
Veja que se m>(2/3), teremos uma função crescente, e dado os valores:
(3m-2) > 0; (2m)>0, 3m >0
Assim, não teremos uma solução para m>(2/3)
E caso todos os valores forem negativos, então
(3m-2)<0, 2m<0, 3m<0
E então não teria solução também.
E não podemos admitir o valor de (2/3), pois a anularia a equação de segundo grau.
Assim:
Veja que só tem um ponto de encontro, assim, o valor de Delta equivale a zero.
Portanto:
Assim, m=0
Pra saber se cumpre, podemos descobrir o valor de x quando toca no ponto y=0
Se a solução está entre -1 e 0, então:
Portanto, m só pode ser 0. E então a equação fica com cara:
Carlos Adir- Monitor
- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
agradecimento
por Darienzo Seg 06 Out 2014, 18:13
Ao Carlos Adir, obrigada pela resposta. Só estou meio confusa é com a resposta do livro :0
Darienzo- Iniciante
- Mensagens : 8
Data de inscrição : 17/09/2014
Idade : 73
Localização : cuiabá, Mato Grosso, Brasil.
Re: Equação do 2º grau
por Carlos Adir Seg 06 Out 2014, 21:38
Qual seria a resposta do livro? Eu fiz de dois modos acima.
Um considerando que existe apenas uma solução:
(x-a)(x-a)=0
Ou seja, Delta equivale a zero.
Outro que considera o valor de x entre -1 e 0. Assumindo x=-1, tem-se o mínimo, e assumindo x=0, teremos o máximo possivel.
Assim, era apenas possivel a solução x=0
Um considerando que existe apenas uma solução:
(x-a)(x-a)=0
Ou seja, Delta equivale a zero.
Outro que considera o valor de x entre -1 e 0. Assumindo x=-1, tem-se o mínimo, e assumindo x=0, teremos o máximo possivel.
Assim, era apenas possivel a solução x=0
____________________________________________
← → ↛ 
⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ º ª ⁿ ⁱ
₀ ₁ ₂ ₃ ₄ ₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ₐ ₑ ₒ ₓ ₔ
∴ ≈ ≠ ≡ ≢ ≤ ≥ × ± ∓ ∑ ∏ √ ∛ ∜ ∝ ∞
∀ ∃ ∈ ∉ ⊂ ⊄ ⋂ ⋃ ∧ ∨ ℝ ℕ ℚ ℤ ℂ
⊥ ║ ∡ ∠ ∢ ⊿ △ □ ▭ ◊ ○ ∆ ◦ ⊙ ⊗ ◈
Αα Ββ Γγ Δδ Εε Ζζ Ηη Θθ Ιι Κκ Λλ Μμ Νν Ξξ Οο Ππ Ρρ Σσς Ττ Υυ Φφ Χχ Ψψ Ωω ϑ ϒ ϖ ƒ ij ℓ
∫ ∬ ∭ ∳ ∂ ∇
ℛ ℜ ℰ ℳ ℊ ℒ
Carlos Adir- Monitor
- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
resposta do livro
por Darienzo Ter 07 Out 2014, 09:52
Carlos, a resposta é 0 < m < 1/2, do livro: vol. 1 Gelson Iezzi e Carlos Murakami, (conjuntos e funções), exercício
pág.179, nº 342.
pág.179, nº 342.
Darienzo- Iniciante
- Mensagens : 8
Data de inscrição : 17/09/2014
Idade : 73
Localização : cuiabá, Mato Grosso, Brasil.
Re: Equação do 2º grau
por Elcioschin Ter 07 Out 2014, 11:19
Darienzo
Não faça formatação para o tamanho de letra, pois fica difícil de ler.
Use a letra padrão do fórum, ao digitar.
Você no está respeitando a Regra XI do fórum: sabia a resposta e não postou JUNTO com o enunciado:
Por favor, leia TODAS as Regras do fórum e siga-as nas próximas postagens, para evitar que suas questões sejam bloqueadas.
Não faça formatação para o tamanho de letra, pois fica difícil de ler.
Use a letra padrão do fórum, ao digitar.
Você no está respeitando a Regra XI do fórum: sabia a resposta e não postou JUNTO com o enunciado:
Por favor, leia TODAS as Regras do fórum e siga-as nas próximas postagens, para evitar que suas questões sejam bloqueadas.
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Equação do 2º grau
por Carlos Adir Ter 07 Out 2014, 12:49
Se há uma unica raiz, então teria-se no máximo 2 valores para m.
Como está descrito no enunciado, "para que tenha uma única raíz".
Não seria um intervalo 0
Pelo que tu estás dizendo, para 0
Ou seja, ou o enunciado está errado ao dizer que há apenas uma raiz, ou é o gabarito o errado.
Como está descrito no enunciado, "para que tenha uma única raíz".
Não seria um intervalo 0
Pelo que tu estás dizendo, para 0
Ou seja, ou o enunciado está errado ao dizer que há apenas uma raiz, ou é o gabarito o errado.
Carlos Adir- Monitor
- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
Re: Equação do 2º grau
por Elcioschin Ter 07 Out 2014, 13:41
O enunciado não diz que existe "uma única raiz": ele diz que "existe uma única raiz no intervalo (-1, 0)". Assim, pode existir outra raiz fora deste intervalo.
Gabarito ---> 0 < m < 1/2 ---> Vamos fazer m = 1/4para testar:
[3.m - 2].x² + 2.m.x + 3.m = 0
[3.(1/4) - 2].x² + 2.(1/4).x + 3.(1/4) = 0
- (5/4).x² + (2/4).x + 3/4 = 0
5x² - 2x - 3 = 0 ---> ∆ = b² - 4ac ---> ∆ = (-2)² - 4.5.(-3) ---> ∆ = 64 ---> √∆ = 8
Raízes ---> x' = (2 + 8 )/2.5 ---> x' = 1 ---> x" = (2 - 8 )/2.5 ---> x" = - 0,6
A raiz x" = - 0,6 é a única dentro do intervalo (x' = 1 está fora do intervalo)
Gabarito ---> 0 < m < 1/2 ---> Vamos fazer m = 1/4para testar:
[3.m - 2].x² + 2.m.x + 3.m = 0
[3.(1/4) - 2].x² + 2.(1/4).x + 3.(1/4) = 0
- (5/4).x² + (2/4).x + 3/4 = 0
5x² - 2x - 3 = 0 ---> ∆ = b² - 4ac ---> ∆ = (-2)² - 4.5.(-3) ---> ∆ = 64 ---> √∆ = 8
Raízes ---> x' = (2 + 8 )/2.5 ---> x' = 1 ---> x" = (2 - 8 )/2.5 ---> x" = - 0,6
A raiz x" = - 0,6 é a única dentro do intervalo (x' = 1 está fora do intervalo)
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Equação do 2º grau
por Darienzo Qua 08 Out 2014, 10:11
Elciochim, peço desculpas pelos erros que cometi, vou ficar mais atenta. O meu problema é que não sou uma expert no computador e muitas vezes não sei achar o que preciso.
Me desculpe.
Me desculpe.
Darienzo- Iniciante
- Mensagens : 8
Data de inscrição : 17/09/2014
Idade : 73
Localização : cuiabá, Mato Grosso, Brasil.
Re: Equação do 2º grau
por Darienzo Qui 27 Nov 2014, 18:57
onde acho "parar de monitorar este tópico"
Darienzo- Iniciante
- Mensagens : 8
Data de inscrição : 17/09/2014
Idade : 73
Localização : cuiabá, Mato Grosso, Brasil.
Tópicos semelhantesPiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
