Canadá

Resolva em  a equação .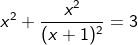

Não tenho gabarito.

Olá.

x² + x²/(x+1)² = 3 .:. x²/x² + x²/[ (x+1)²*x² ] = 3/x² .:. 
1 + 1/(x+1)² = 3/x² .:. x²*(x+1)² + x² = 3*(x+1)² .:. 
x²*(x²+2x+1) + x² = 3*(x²+2x+1) .:. x^4 + 2x³ + x² + x² = 3x²+6x+3 .:. 
x^4+2x³-x²-6x-3 = 0 .:. x^4 - x³ - x² + 3x³-6x-3 = 0 .:. 
x²*(x²-x-1) + 3x³ - 6x - 3 = 0 .:. 
x²*(x²-x-1) + 3x³ - 3x² - 3x + 3x²-3x - 3 = 0 .:. 
x²*(x²-x-1) + 3x*(x²-x-1) + 3*(x²-x-1) = 0 .:. 
(x²+3x+3)*(x²-x-1) = 0 

x²+3x+3 = 0 --> só tem raízes complexas
x²-x-1 = 0 --> x = (1 +- √5)/2


Outra maneira de fatorar é usar aquela mesma ideia dos outros exercícios:


x^4+2x³-x²-6x-3 = (x²+ax-1)*(x²+bx+3)

x^4+2x³-x²-6x-3 = x^4 + bx³ + 3x²+ax³+abx²+3ax-x²-bx-3 .:. 
x^4+2x³-x²-6x-3 = x^4 + (a+b)x³ -(-ab+1)x² - x*(-3a+b) - 3

a+b = 2
-3a+b = 6

--> (-3a+b) - (a+b) = 6 - 2 .:. -4a = 4 .:. a = -1 --> b = 3

Att.,
Pedro

Show, brigadão Pedro.