Hipérbole

Dada a hipérbole 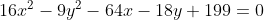, determine as assíntotas da hipérbole.

16x² - 64x + 64 - 9y² - 18y - 9 + 199 = + 64 - 9

16*(x - 2)² - 9*(y - 1)² + 199 = 55

9*(y - 1)² - 16*(x - 2)² = 144

(y - 1)/4² - (x - 2)²/3² = 1 ----> Equação reduzida da hipérbole:

Note que a hipérbole tem eixo real paralelo ao eixo Y

Centro C(2, 1)
Semi-eixo real ----> a = 4
Semi-eixo imaginário ----> b = 3
Distância focal ----> c² = a² + b² ----> c² = 42 + 3² ----> c = -5 e c = +5
Focos ----> F1 (2, -4) e F2 (2, 6)

Faça agora um bom desenho.

Uma assíntota passa pelo centro C(2, 1) e pelo ponto P(5, 6):

y - 1 = [(6 - 1)/(5 - 2)]*(x - 2) -----> 5x - 3y + 7 = 0

A outra passa pelo centro e pelo ponto Q(-1, 6)

Deixo para vc calcular a equação dela.

Por favor corrija minhas contas.