Área por Integral

por matheus_feb Hoje à(s) 21:12

Voltei recentemente aos estudos de Cálculo e decidi experimentar provar algumas fórmulas básicas de áreas de figuras. Entretanto, embora tenha encontrado uma fórmula válida e funcional para o trapézio, ela não está no formato padrão como conhecemos $Área por Integral Gif.latex?A%20=%20\frac{(B%20+%20b)%20$ . Provavelmente errei algo bobo, mas alguém pode me ajudar?

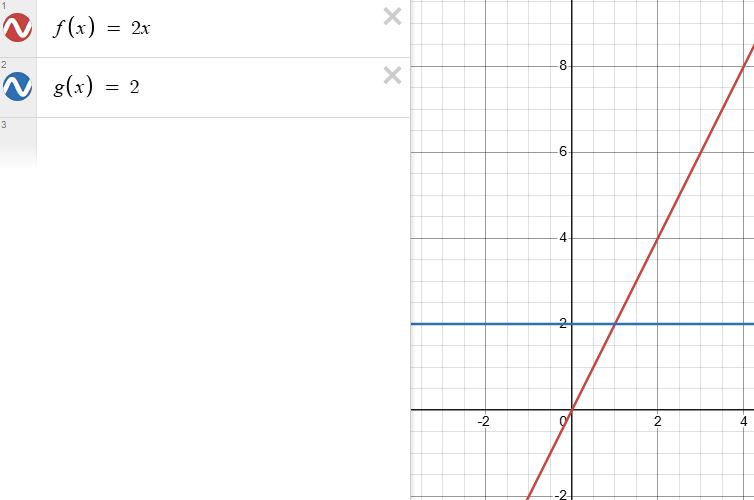
- Supondo a ordenada 2 (igual a g(x)) como sendo h (a altura do trapézio).
- Supondo x = 1 igual a ''v''
- Supondo x = 2 igual a ''w''

Primeiro para a área entre os intervalos, para x, de 0 até v:

$Área por Integral Gif$ $Área por Integral Gif$ $Área por Integral Gif$

Agora para a área entre os intervalos, para x, de v até w:

$Área por Integral Gif$ $Área por Integral Gif$ $Área por Integral Gif.latex?\rightarrow%20\int_{\%20v}^{w}%20h.(w)%20-%20h$ $Área por Integral Gif$ $Área por Integral Gif$

Resultando na equação → Área_(trapézio)= v²+ h(w - v)

Calculando, encontramos A = 1²+ 2(2 -1) = 3

Pela fórmula tradicional, encontramos A = [(2+1) . 2]/2 = 3

Que manipulações algébricas preciso fazer para chegar na fórmula padrão?

por **Giovana Martins** Hoje à(s) 22:05

Por uma questão geométrica, acredito que fique mais fácil dizer que uma das bases está sobre y = y₁ e a outra está sobre y = y₂, ao invés de dizer que uma está sobre y = 0 e a outra sobre y = v.

Nota: y₁ é a base maior e y₂ é a base menor. Tente deste jeito.

por matheus_feb Hoje à(s) 22:21

Giovana Martins escreveu:
Por uma questão geométrica, acredito que fique mais fácil dizer que uma das bases está sobre y = y₁ e a outra está sobre y = y₂, ao invés de dizer que uma está sobre y = 0 e a outra sobre y = v.

Nota: y₁ é a base maior e y₂ é a base menor. Tente deste jeito.

Já consegui. Muito obrigado!

lol!

por **Elcioschin** Hoje à(s) 22:27

Basta integrar entre os limites 1, 2

S = x² ---> entre limites ---> S = 2² - 1² ---> S = 3

por **Giovana Martins** Hoje à(s) 22:30

Para não dizer que eu estou "acochambrando", vou fazer com a base posicionada sobre o eixo x.

Sejam os pontos (0,0), (x₁,y₁), (x₂,y₁), (x₃,0), (x₂,0) e (x₁,0), com x₁ < x₂ < x₃.

A reta formada por (0,0) e (x₁,y₁) é dada por:

\[\mathrm{y=\frac{y_1}{x_1}x}\]

A reta formada por (x₁,y₁) e (x₂,y₁) é dada por:

\[\mathrm{y=y_1}\]

A reta formada por (x₂,y₁) e (x₃,0) é dada por:

\[\mathrm{y=\frac{y_1}{x_2-x_3}(x-x_3) }\]

A área, portanto, é dada por:

\[\mathrm{A=\int_{0}^{x_1}\left ( \frac{y_1}{x_1}x \right )dx+\int_{x_1}^{x_2}(y_1)dx+\int_{x_2}^{x_3}\left [ \frac{y_1}{x_2-x_3}(x-x_3) \right ]dx}\]

\[\mathrm{A=\frac{1}{2}(x_3+x_2-x_1)y_1}\]

Naturalmente, x₂ - x₁ é a base menor e aí é só questão de nomenclatura.

por **Giovana Martins** Hoje à(s) 22:32

Só confira as continhas, pois posso ter confundido algum índice entre 1, 2 e 3.

por matheus_feb Hoje à(s) 22:33

Elcioschin escreveu:Basta integrar entre os limites 1, 2

S = x² ---> entre limites ---> S = 2² - 1² ---> S = 3

Na verdade, minha dúvida estava na elaboração da fórmula da área de um trapézio a partir de Integrais. Mas já consegui sanar essa questão por conta própria. Obrigado!

por matheus_feb Hoje à(s) 22:41

Giovana Martins escreveu:
Para não dizer que eu estou "acochambrando", vou fazer com a base posicionada sobre o eixo x.

Sejam os pontos (0,0), (x₁,y₁), (x₂,y₁), (x₃,0), (x₂,0) e (x₁,0), com x₁ > x₂ > x₃.

A reta formada por (0,0) e (x₁,y₁) é dada por:

\[\mathrm{y=\frac{y_1}{x_1}x}\]

A reta formada por (x₁,y₁) e (x₂,y₁) é dada por:

\[\mathrm{y=y_1}\]

A reta formada por (x₂,y₁) e (x₃,0) é dada por:

\[\mathrm{y=\frac{y_1}{x_2-x_3}(x-x_3) }\]

A área, portanto, é dada por:

\[\mathrm{A=\int_{0}^{x_1}\left ( \frac{y_1}{x_1}x \right )dx+\int_{x_1}^{x_2}(y_1)dx+\int_{x_2}^{x_3}\left [ \frac{y_1}{x_2-x_3}(x-x_3) \right ]dx}\]

\[\mathrm{A=\frac{1}{2}(x_3+x_2-x_1)y_1}\]

Naturalmente, x₂ - x₁ é a base menor e aí é só questão de nomenclatura.

Tudo certo. Obrigado pela resolução, bem elegante!

por **Giovana Martins** Hoje à(s) 23:02

matheus_feb escreveu:
Giovana Martins escreveu:
Para não dizer que eu estou "acochambrando", vou fazer com a base posicionada sobre o eixo x.

Sejam os pontos (0,0), (x₁,y₁), (x₂,y₁), (x₃,0), (x₂,0) e (x₁,0), com x₁ > x₂ > x₃.

A reta formada por (0,0) e (x₁,y₁) é dada por:

\[\mathrm{y=\frac{y_1}{x_1}x}\]

A reta formada por (x₁,y₁) e (x₂,y₁) é dada por:

\[\mathrm{y=y_1}\]

A reta formada por (x₂,y₁) e (x₃,0) é dada por:

\[\mathrm{y=\frac{y_1}{x_2-x_3}(x-x_3) }\]

A área, portanto, é dada por:

\[\mathrm{A=\int_{0}^{x_1}\left ( \frac{y_1}{x_1}x \right )dx+\int_{x_1}^{x_2}(y_1)dx+\int_{x_2}^{x_3}\left [ \frac{y_1}{x_2-x_3}(x-x_3) \right ]dx}\]

\[\mathrm{A=\frac{1}{2}(x_3+x_2-x_1)y_1}\]

Naturalmente, x₂ - x₁ é a base menor e aí é só questão de nomenclatura.
Tudo certo. Obrigado pela resolução, bem elegante!

Quando você avançar mais nos estudos, dê uma procurada na demonstração da área de uma elipse. É muito bonita a demonstração (na minha opinião).

Utiliza o conceito de substituições trigonométricas. Não chega a ser difícil, e você também não está distante na teoria até chegar neste tópico. Mas é claro, cuidado para não andar demais pela área de cálculo em detrimento do vestibular (sei que você não pediu o conselho).