Produtos Notáveis
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Produtos Notáveis
por caiolira09 Qua 07 maio 2014, 10:18
Alguém me pode me ajudar? Quebrei a cabeça um tempão nesse exercício e até agora nada.
Sejam x e y números reais tais qu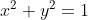e
e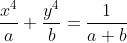 
. O valor de 
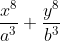é igual a:
a)
b) 
c) 
d)
e) 
Sejam x e y números reais tais que
a)
d)
caiolira09- Iniciante
- Mensagens : 5
Data de inscrição : 07/03/2014
Idade : 30
Localização : Rio de Janeiro, Rio de Janeiro, Brasil.
Re: Produtos Notáveis
por Luck Qua 07 maio 2014, 17:54
Como x² + y² = 1 , para facilitar vamos fazer uma substituição trigonométrica, seja x = senθ , y = cosθ , temos: [(senθ)^4]/a + [(cosθ)^4]/b = 1/(a+b)
b(sen²θ)² + a(cos²θ)² = ab/(a+b)
b(sen²θ)² + a (1-sen²θ)² = ab/(a+b)
b(sen²θ)² + a(1 -2sen²θ + (sen²θ)² ) = ab/(a+b)
(a+b)(sen²θ)² -(2a)sen²θ + a - (ab/(a+b) = 0
(a+b)(sen²θ)² - (2a)sen²θ + a²/(a+b) = 0
∆ = 4a² - 4(a+b)a²/(a+b)
∆ = 0
sen²θ = 2a/2(a+b) = a/(a+b) ∴ cos²θ = b/(a+b)
S = [(x^8)/a³] + (y^8)/b³
S= [(sen²θ)^4/ a³] + [ (cos²θ)^4 / b³ ]
S = [a/(a+b)^4] + [b/(a+b)^4]
S = (a+b)/(a+b)^4
S = 1/(a+b)³
b(sen²θ)² + a(cos²θ)² = ab/(a+b)
b(sen²θ)² + a (1-sen²θ)² = ab/(a+b)
b(sen²θ)² + a(1 -2sen²θ + (sen²θ)² ) = ab/(a+b)
(a+b)(sen²θ)² -(2a)sen²θ + a - (ab/(a+b) = 0
(a+b)(sen²θ)² - (2a)sen²θ + a²/(a+b) = 0
∆ = 4a² - 4(a+b)a²/(a+b)
∆ = 0
sen²θ = 2a/2(a+b) = a/(a+b) ∴ cos²θ = b/(a+b)
S = [(x^8)/a³] + (y^8)/b³
S= [(sen²θ)^4/ a³] + [ (cos²θ)^4 / b³ ]
S = [a/(a+b)^4] + [b/(a+b)^4]
S = (a+b)/(a+b)^4
S = 1/(a+b)³
Luck- Grupo
Velhos amigos do Fórum
- Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 32
Localização : RJ
caiolira09- Iniciante
- Mensagens : 5
Data de inscrição : 07/03/2014
Idade : 30
Localização : Rio de Janeiro, Rio de Janeiro, Brasil.
Re: Produtos Notáveis
por jarry15 Qui 08 maio 2014, 01:36
Noossa tentei bastante, jamais ia conseguir sem estar por dentro de trig... . =P
jarry15- Recebeu o sabre de luz
- Mensagens : 115
Data de inscrição : 17/04/2014
Idade : 30
Localização : Boa Vista, RR, BR
Re: Produtos Notáveis
por caiolira09 Qui 08 maio 2014, 09:32
Na verdade depois eu pesquisei e encontrei três outras formas de resolver. Por desigualdade de Cauchy-Schwarz, fazendo uma equação na outra (que da muito trabalho) e utilizando uma técnica que alguns chamam de "Um lema poderoso" onde 
, mas a resolução que o Luck fez também é rápida e prática, além de ser muito mais justa.
caiolira09- Iniciante
- Mensagens : 5
Data de inscrição : 07/03/2014
Idade : 30
Localização : Rio de Janeiro, Rio de Janeiro, Brasil.
Tópicos semelhantes» Produtos Notáveis
» Produtos Notáveis V
» Produtos notáveis.
» Produtos notáveis
» (CN) Produtos Notaveis
» Produtos Notáveis V
» Produtos notáveis.
» Produtos notáveis
» (CN) Produtos Notaveis
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
