Losango
3 participantes
Página 1 de 1
Losango
por SirHipotenusa Ter 29 Abr 2014, 19:53
Um losango ABCD, em que o angulo A=60º, é cortado por retas paralelas a AB e AD que distam respectivamente destes lados 2cm e 3cm. Se a maior diagonal mede 12cm, qual a distancia do ponto de intersecção das paralelas à menor diagonal?
R: 1cm
R: 1cm
SirHipotenusa- Padawan
- Mensagens : 71
Data de inscrição : 10/10/2013
Idade : 26
Localização : Brasil, Rio de Janeiro e Rio de Janeiro
Re: Losango
por Elcioschin Qua 30 Abr 2014, 15:05
Use o desenho para completar a questão por GA
[IMG]https://2img.net/h/oi59.tinypic.com/2e4cbr9.gif[/I
[IMG]https://2img.net/h/oi59.tinypic.com/2e4cbr9.gif[/I
Elcioschin- Grande Mestre
- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
raimundo pereira- Grupo
Velhos amigos do Fórum
- Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Re: Losango
por SirHipotenusa Seg 05 maio 2014, 19:15
Muito obrigado. Não consegui entender muito bem a sua forma de pensamento, mas vou olhar com mais atenção. De qualquer forma, agradeço a resposta.
SirHipotenusa- Padawan
- Mensagens : 71
Data de inscrição : 10/10/2013
Idade : 26
Localização : Brasil, Rio de Janeiro e Rio de Janeiro
Re: Losango
por raimundo pereira Seg 05 maio 2014, 20:48
Vamos tentar detalhar:
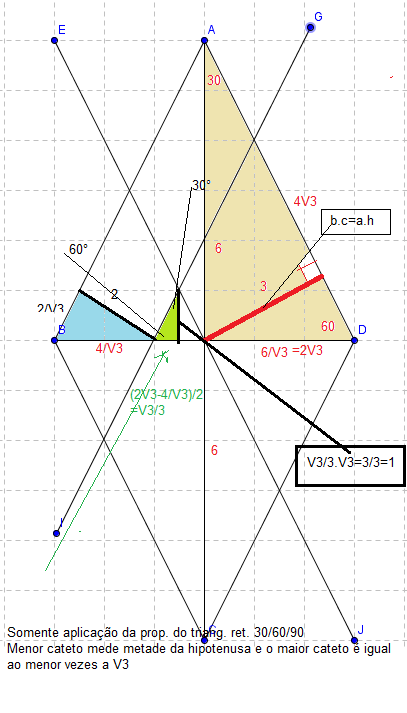
1-Feito o desenho, trace as paralelas conforme o enunciado e marque as distancias(perpendiculares) dadas (2) e (3 ) perpend. a AB e CD respect.
2 - Considerando "O" o centro do losango , veja que o triâng. AOC é ret. com ângs. 30/60/90. Como a maior diagonal mede 12 , o cateto maior de AOD mede 6 e o menor mede 2/V3=2V3 , e a hipot. mede 2 vezes o menor cateto=(4V3).
3 - A distancia da paralela ao lado AD pode ser obtida aplicando-se a rel met. no triâng. ret b.c=a.h
4 - Observe que OB=OD=2V3.
5 - A distancia ao lado AB(2), determina o triâng. ret. 30/60/90 ( em azul).
6 - Nesse triâng. ret. 30/60/90 , se o maior cateto mede 2 o menor mede 2/V3 e a hipot. mede 2.2/V3=4/V3. Como OB mede 2V3 temos que a base do triâng. menor (metade verde) mede OB - 4/V3 . Como queremos a dist da diagonal menor ao ponto de concurso das paralelas observe que essa dist. corresponde ao maior cateto do triang. ret 30/60/90 em verde).
QQ dúvida pergunte.
1-Feito o desenho, trace as paralelas conforme o enunciado e marque as distancias(perpendiculares) dadas (2) e (3 ) perpend. a AB e CD respect.
2 - Considerando "O" o centro do losango , veja que o triâng. AOC é ret. com ângs. 30/60/90. Como a maior diagonal mede 12 , o cateto maior de AOD mede 6 e o menor mede 2/V3=2V3 , e a hipot. mede 2 vezes o menor cateto=(4V3).
3 - A distancia da paralela ao lado AD pode ser obtida aplicando-se a rel met. no triâng. ret b.c=a.h
4 - Observe que OB=OD=2V3.
5 - A distancia ao lado AB(2), determina o triâng. ret. 30/60/90 ( em azul).
6 - Nesse triâng. ret. 30/60/90 , se o maior cateto mede 2 o menor mede 2/V3 e a hipot. mede 2.2/V3=4/V3. Como OB mede 2V3 temos que a base do triâng. menor (metade verde) mede OB - 4/V3 . Como queremos a dist da diagonal menor ao ponto de concurso das paralelas observe que essa dist. corresponde ao maior cateto do triang. ret 30/60/90 em verde).
QQ dúvida pergunte.
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
