Produtos Notáveis/ Fatoração

por L.Lawliet Dom 27 Abr 2014, 09:38

Dada as relações:

1- $\left [ \left ( \frac{x}{\sqrt{y}} \right )^3 + \left ( \frac{y}{\sqrt{x}} \right )^3 \right ] \right ]^2 + \left [ \left ( \frac{x}{\sqrt{y}} \right )^3 - \left ( \frac{y}{\sqrt{x}} \right )^3 \right ] \right ]^2 = 10(x^3+y^3)$

2- $x^6-y^6=6x^4y^4 (\sqrt[3]{x^3+y^3})$

Calcule:

$\frac{3}{x^-^3-y^-^3}$

A resposta é -1

por William Lima Dom 27 Abr 2014, 16:53

Livro peruano?

por L.Lawliet Dom 27 Abr 2014, 16:54

sim, voce sabe fazer william?

por PedroCunha Seg 28 Abr 2014, 21:01

Alguém?

por L.Lawliet Seg 28 Abr 2014, 21:57

Pedro, eu desenvolvi a 1ª relação da seguinte forma:

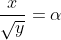
$\frac{x}{\sqrt{y}}=\alpha$

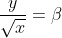
$\frac{y}{\sqrt{x}}=\beta$

Dai fiz:

$\left \lfloor \alpha ^3+\beta ^3 \right \rfloor^2 + \left \lfloor \alpha ^3-\beta ^3 \right \rfloor^2 = 2\left ( \alpha ^6+\beta ^6 \right )=10(x^3+y^3)$

Tirando o MMC e fatorando, obtive:

$\frac{x^9+y^9}{x^3y^3}=5(x^3+y^3)$

Fatorando novamento, econtrei :

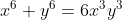
$x^6+y^6=6x^3y^3$

Mas não consigo desenvolver mais nada que pareça util. Pelo gabarito, parece que voce precisa achar que (x³y³)/(y³-x³)= -1/3. Mas eu não consigo desenvolver nada que me leve a essa conclusão. Se alguem tiver alguma ideia, ajuda ai Very Happy

por Luck Ter 29 Abr 2014, 02:27

C.E: x > 0 , y > 0 , x > y.
x^6 + y^6 = 6x³y³ (I)
(x³+y³)² -2x³y³ = 6x³y³
(x³+y³)² = 8x³y³
∛(x³+y³)² = 2xy (II)

x^6 - y^6 = 6(x^4)(y^4)∛(x³+y³)
elevando ao quadrado:
(x^6 - y^6)² = 36(x^8)(y^8)∛(x³+y³)²
substituindo (II):
(x^6 - y^6)² = 72(x^9)(y^9) (III)

(I)² :
(x^6 + y^6)² = 36(x^6)(y^6) (IV)
subtraindo (IV) de (III):
4(x^6)(y^6) = 36(x^6)(y^6) - 72(x^9)(y^9)
72(x^9)(y^9) =32(x^6)(y^6)
x³y³ = 4/9 ∴ xy = ∛(4/9)

de (II) :
(x³+y³)² = 8x³y³ ∴ (x³+y³)² = 32/9 ∴ (x³+y³) = 4√2/3

x^6 - y^6 = 6(x^4)(y^4)∛(x³+y³)
(x³+y³)(x³-y³) = 6x³y³(xy)∛(x³+y³)
[(4√2)/3](x³-y³) = 6(4/9)∛(4/9)∛(4√2/3)
fazendo as contas vc vai obter x³ - y³ = 4/3

S = 3/[(1/x³) -(1/y³)] = 3x³y³/(y³-x³)
S = 3(4/9)/(-4/3)
S = -1

chatinha..