(Mackenzie) Prismas
2 participantes
Página 1 de 1
(Mackenzie) Prismas
por perlingra Ter 04 Mar 2014, 20:22
As medidas das arestas de um paralelepípedo retângulo estão em
[ltr]P.G.[/ltr]
, sabendo-se que a diagonal desse paralelepípedo retângulo mede
e que a soma de todas as arestas é 
então podemos afirmar que o volume desse sólido é:
\,%2054cm^3)
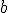\,%2091cm^3)
\,%2027cm^3)
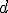\,%20169cm^3)
\,%2052sqrt%20{91})
[ltr]P.G.[/ltr]
, sabendo-se que a diagonal desse paralelepípedo retângulo mede
perlingra- Recebeu o sabre de luz
- Mensagens : 154
Data de inscrição : 16/08/2012
Idade : 28
Localização : São Luís, MA, Brasil
Re: (Mackenzie) Prismas
por PedroCunha Ter 04 Mar 2014, 22:19
Olá.
Sejam as arestas a,b e c.
Do enunciado, podemos falar que b² = ac (P.G.)
Diagonal = √(91):
√(a²+b²+c²) = 91 .:. a²+b²+c² = 91
Soma de todas as arestas = 52:
4a + 4b + 4c = 52 .:. a + b + c = 13, a+c = 13-b
Lembrando agora do produto notável: a²+b²+c² = (a+b+c)² - 2*(ab+bc+ac), temos:
13² - 2*(b*(a+c) + b²) = 91 .:. 169 - 2*(b*(13-b) + b²) = 91 .:. 78 = 2*(13b - b²+b²) .:.
39 = 13b .:. b = 3
Lembrando que o volume do paralelepípedo é a*b*c, temos:
V = a*b*c .:. V = b*(a*c) .:. V = b*b² .:. V = b³ .:. V = 3³ .:. V = 27cm³
Att.,
Pedro
Sejam as arestas a,b e c.
Do enunciado, podemos falar que b² = ac (P.G.)
Diagonal = √(91):
√(a²+b²+c²) = 91 .:. a²+b²+c² = 91
Soma de todas as arestas = 52:
4a + 4b + 4c = 52 .:. a + b + c = 13, a+c = 13-b
Lembrando agora do produto notável: a²+b²+c² = (a+b+c)² - 2*(ab+bc+ac), temos:
13² - 2*(b*(a+c) + b²) = 91 .:. 169 - 2*(b*(13-b) + b²) = 91 .:. 78 = 2*(13b - b²+b²) .:.
39 = 13b .:. b = 3
Lembrando que o volume do paralelepípedo é a*b*c, temos:
V = a*b*c .:. V = b*(a*c) .:. V = b*b² .:. V = b³ .:. V = 3³ .:. V = 27cm³
Att.,
Pedro
PedroCunha- Monitor
- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
