Módulo

(Ufrj) Seja f a função real dada por f(x) = ax² + bx + 
c, com a > 0. Determine a, b e c sabendo que as 
raízes da equação | f (x) | = 12 são -2, 1, 2 e 5. 
Justifique.

resposta : a = 2, b = - 6, c = - 8

me expliquem passo a passo por favor
a minha primeira dúvida nesse problema e como que vou saber que raíz é de qual equação.

se módulo de f(x) é igual a 12, concorda que ou f(x) = 12 ou f(x) = -12? Então:

------->  f(x) = 12
ax² + bx + c = 12
ax² + bx + c - 12 = 0


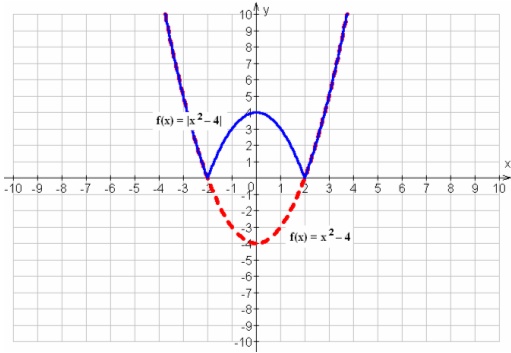
Pela imagem perceba que as raízes da extremidade (-2 e 5) são da função sem módulo e as raízes do meio (1 e 2) são da função oposta.

As raízes são -2 e 5
a(-2)² + b(-2) + c - 12 = 0
-> 4a - 2b + c = 12 (I)

5²a + 5b + c - 12 = 0
-> 25a + 5b +c = 12 (II)


---------> f(x) = -12
ax² + bx + c = -12
ax² + bx + c + 12 = 0
Raízes 1 e 2
-> a + b + c = -12 (III)
-> 4a + 2b + c = -12 (IV)


Resolvendo o sistema composto por (I), (II), (III) e (IV), temos que a = 2, b = - 6, c = - 8.

Entendi obrigada!
entao para achar as raízes o único jeito é desenhar?

Não entendi o gráfico,alguém pode me explicar como surgiu esse F=|x²-4|.

Eu também não entendi. No gráfico as raízes parecem ser -2 e 2 apenas

Vamos começar do zero:

Temos a função f(x) = a.x² + b.x + c ---> com a > 0

O gráfico da função é uma parábola com a concavidade voltada para cima. Seja xV a abcissa do vértice.

|f(x)| = 12 --> raízes -2, 1, 2, 5 --->
Sejam M e N os pontos médios das raízes(1, 2) e (-2, 5), respectivamente:

xM = (1 + 2)/2 ----> xM = 3/2
xN = (-2 + 5)/2 ---> xN = 3/2

Conclusão:  xM = xN = xV ---> xV = 3/2 ---> -b/2.a = 3/2 ---> b = -3.a ---> I

Temos duas possibilidades para o módulo:

1) f(x) = - 12 ---> a.x² + b.x + c = - 12 ---> a.x² - 3a.x + c = - 12

Para x = 1 ---> a.1² - 3.a.1 + c = - 12 ---> -2.a + c = - 12 ---> II

Para x = 2 obteríamos a mesma equação II

2) f(x) = + 12 ---> a.x² + b.x + c = 12 ---> a.x² - 3a.x + c = 12

Para x = -2 ---> a.(-2)² - 3.a.(-2) + c = 12 ---> 10.a + c = 12 ---> III

Para x = 5 obteríamos a mesma equação III

III - II ---> (10.a + c) - (-2a + c) = 12 - (-12) ---> a = 2

I ---> b = -3.a --> b = -3.2 ---> b = -6

III ---> 10.a + c = 12 ---> 10.2 + c = 12 ---> c = -8

f(x) = 2.x² - 6.x - 8

Élcio, por que você escolheu os pontos médios das raízes(1, 2) e (-2, 5)?

Não entendi....

Porque o ponto médio das duas raízes de uma parábola é a abcissa do vértice da parábola!!! Isto acontece porque a parábola é uma curva simétrica em relação ao seu eixo de simetria, que passa pelo seu vértice.
Você não sabia disso???

Elcioschin escreveu:Porque o ponto médio das duas raízes de uma parábola é a abcissa do vértice da parábola!!! Isto acontece porque a parábola é uma curva simétrica em relação ao seu eixo de simetria, que passa pelo seu vértice.
Você não sabia disso???

Já a minha duvida é parecida com a dele; porque foi escolhido raízes(1, 2) e (-2, 5) e não (1,5) e (-2,2) ?
e o senhor usou Xv somente para definir o coeficiente b para em seguida montar os 3 sistemas?

Porque ambas as equações representam pontos diferentes de uma mesma parábola (y = 12 e y = -12), a qual tem vértice V(xV, yV) onde xV = - b/2.a