Polinômio quadrado perfeito

Calcule p para que o polinômio

4x^4 -8x³ + 8x² - 4(p-1)x + (p-1)²

seja o quadrado perfeito de um polinômio racional inteiro em x.

Resp: p = 0

seja P(x) = ax^2 + bx + c. Queremos que 
4x^4 -8x³ + 8x² - 4(p-1)x + (p-1)² = 
=(ax^2 + bx + c)^2


(De fato, o polinômio escolhido tem que ser de grau 2, já que temos um grau 4 ali, certo?)


Assim, expandindo o trinômio:






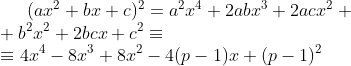
Da identidade de polinômios:
a=+/- 2
c=(p-1)
2abx = -8 <=> b=-2 ou b= 2

Se a=2:

2.a.c + (b)^2 = 8 <=>  4(p-1) = 4 <=> p = 2

Expanda (2x^2 - 2x + 2)^2 e veja se da certo.

Se = -2, c=0. Expanda e veja o que acontece, da mesma forma

a²x^4 + 2abx³ + (2ac + b²)x² + 2bcx + c² = 4x^4 - 8x³ + 8x² - 4(p-1)x + (p-1)²

Aplicando o teorema da igualdade de polinômios: 

a² = 4 -> a = +/- 2
2ab = -8 (I)
2ac + b² = 8 (II)
2bc = -4(p-1) (III)
c² = (p-1)² (IV)

Com a = 2, b = -8/4 = -2; c = 8-(-2)² / 4 = 1 e p = 2

Daí, teríamos (2x² - 2x + 1)². Desenvolvendo, obtemos 4x^4 - 8x³ + 4x² + 1 (isso não deveria acontecer).

Se a = -2, b = -8/2.-2 = 2; c = 8 - (2²)/2.-2 = 8-4/-4 = 4/-4 = -1 -> p = 0. Isso implica no polinômio 
(-2x² + 2x - 1)². Desenvolvendo, ficamos com 4x^4 - 8x³ + 8x² - 4x + 1. Isso também não deveria acontecer, pois, se p=0, a1 = 4, não -4. 

Onde estou errando?

Hm tem razão, eu coloquei la em cima o p direto no lugar de c, o que está, obviamente, errado. Foi um erro de notação.

Substituindo p=0 no polinômio:

4x^2 - 8x^3 + 8x^2 - 4(-1)x + 1

Nesse caso teriamos um problema de sinal

Acho que o ue estamos errando é o seguinte:

-4(p-1) = 2bc

Como b>0, teremos c = 1-p (o que confere com IV, já que c^2 = (p-1)^2 <=> c=(p-1) ou c=1-p)

Mas assim eu encontro, da mesma maneira, p = 2 :/

Além disso, esse polinômio tem as 4 raizes complexas (fazendo p=0). Para que ele fosse o quadrado perfeito de algum outro, terismos que ter 2 raizes, ela e seu conjugado (cada uma com multiplicidade 2) . Mas, pelo wolfram, se eu coloquei a equação corretamente, são 4 raizes complexas.

Se eu te disser uma coisa você não vai acreditar: eu copiei o enunciado errado  

O correto é:

4x^4 - 8x³ + 8x² - 4(p+1)x + (p+1)²

Daí, III e IV mudam para:

2bc = -4(p+1) (III)
c² = (p+1)² (IV) 

Então, se colocarmos p=0, teremos o sinal correto em a1. 

Por que b>0? Bom, se b<0, teríamos b = -2, a = 2 e c = 1. Assim, c = p+1 = 1+p -> p = c-1 -> p = 0


Um polinômio quadrado perfeito ax²+bx+c pode ser escrito da forma (px+q)²:

(px+q)² = p²x² + 2pqx + q²

a = p²
b = 2pq
c = q²

Acho que a>0 e c>0, mas b não precisa ser positivo. (nem sei se essa definição de polinômio quadrado perfeito está certa também)

Ah, senhor Gabriel

Disse que b>0 pois já tinhamos o valor de b. Está não é uma condição, de fato.

Última pergunta: todo polinômio quadrado perfeito deve ser da forma (ax² + bx + c)^n ?

Não Gabriel tem que analisar o grau como a Giovanna disse, ali é grau 4 por isso usa um de grau 2 pois ele ao quadrado aparece um de grau 4.

Mas se por exemplo ax²+bx+c é um quadro perfeito, se e somente se existir (px+q)²=ax²+bx+c , se tive dúvidas dá uma olhada no livro do Gelson Iezzi Vol06 parte de polinômios. Abraço!