Binômio

Relembrando a primeira mensagem :

Prove que:

Ficou muito boa a resolução. Aliás, me fez perceber que a minha estava meio sem fundamento. 

Mas qual o termo após o 3° "=" ?

https://2img.net/r/ihimizer/img10/2932/uyuh.jpg 


Ve o link

O link não está abrindo.  

E confirmando: tem um buraco enorme na minha resolução. Está sem fundamento.

kakaroto escreveu:vc escreveu prove, então o certo seria demonstre, pois provar eu provei

 E se tivermos: Prove que  é primo, você garante que testando um número vai generalizar para todo i>0?

O "teste" só da certo pois sabemos que a relação é verdadeira, então para todo n>=2 (no caso deste tópico), teremos que a relação é verdadeira. Mas, quem disse que testando para n será válido para n+1? 

Por isso a importância do princípio da indução finita ou prova algébrica (essa que eu fiz foi algébrica) pois eu garanto que é verdadeira.

Se quiser tentar, o exemplo acima é a prova de que testar não prova nada, já que para i =5 (acho que é isso), esse número já não é primo, mesmo que os anteriores sejam

Até

Veja agora, atualizei la em cima a imagem

Pronto, tá dando pra ver agora. Consegui entender o desenvolvimento. Ficou ótimo, obrigado  

Estava travado neste exercício, mas com aquela relação que você mostrou dá pra resolver vários...

n² - n + 41 é a "fórmula dos números primos" que eu tinha dito.

Se "provar" pra os primeiros naturais, não garante que essa fórmula é válida. (nem deve existir uma equação que gere todos os primos)

Gabriel Rodrigues escreveu:Pronto, tá dando pra ver agora. Consegui entender o desenvolvimento. Ficou ótimo, obrigado  

Estava travado neste exercício, mas com aquela relação que você mostrou dá pra resolver vários...

 Essa relação é uma maravilha, e surge demuma coisa tão básica...

Ela é útil em vários exercícios de combinatória: De quantas maneiras podemos ligar as m  lâmpadas de uma sala?

Vai precisar dela ainda  

Até

Essa relação é muito útil mesmo. Acredito que se houver n lâmpadas na sala, podemos ligar 1, 2, 3, 4, ..., n (todas acesas), que pode ser feito de Cn,1, Cn,2 ... Cn,n. Como os resultados são independentes: Cn,1 + Cn,2 ... + Cn,n. Isso é obtido pela relação:



Também dá pra pensar que temos duas possibilidades para cada lâmpada: acesa ou apagada. Se desconsiderarmos a possibilidade em que todas estão apagadas, vem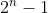   possibilidades. (isso considerarmos todos os interruptores simples, pois se associarmos a alguns paralelos poderemos acender uma lâmpada de mais de um lugar, daí não sei como proceder  ). 

Ela é útil também pra determinarmos o número de eventos de um espaço amostral finito e, enfim, o número de subconjuntos de um conjunto de n elementos. 

Tenho outra: de quantas formas um salão de n portas pode ser aberto?

Isso mesmo.

Essa do salão acredito que é a mesma coisa, considerando que pelo menos uma porta deve ser aberta.

E sim, todos os interruptores são simples. Nem me vennha com essas coisas de físicos