Geometria Plana
2 participantes
Página 1 de 1
Geometria Plana
por Rflbboy Ter 09 Jul 2013, 20:54
Em um triângulo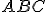 
, considere as alturas 
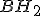e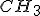 
. Prove que o triângulo 
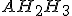é semelhante ao triângulo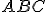
Rflbboy- Iniciante
- Mensagens : 8
Data de inscrição : 06/03/2013
Idade : 30
Localização : Brasil
Re: Geometria Plana
por kakaroto Qua 10 Jul 2013, 01:21
Cara depende do triângulo, pois cada triângulo tem uma demonstração, vou demonstrar em um triângulo isóceles.
essa é a representação das alturas H3 e H2
Percebe como a reta H3H2 é paralela à reta bc ? Portanto os ângulos tbm são indênticos, fazendo o triângulo ser semelhante.
essa é a representação das alturas H3 e H2
Percebe como a reta H3H2 é paralela à reta bc ? Portanto os ângulos tbm são indênticos, fazendo o triângulo ser semelhante.
kakaroto- Mestre Jedi
- Mensagens : 628
Data de inscrição : 01/04/2013
Idade : 30
Localização : São Paulo
Re: Geometria Plana
por Rflbboy Qua 10 Jul 2013, 07:17
Tem como você fazer essa demonstração em um triângulo escaleno acutângulo?
Rflbboy- Iniciante
- Mensagens : 8
Data de inscrição : 06/03/2013
Idade : 30
Localização : Brasil
kakaroto- Mestre Jedi
- Mensagens : 628
Data de inscrição : 01/04/2013
Idade : 30
Localização : São Paulo
Re: Geometria Plana
por Rflbboy Qua 10 Jul 2013, 13:51
Sim, eu estava usando o GeoGebra e percebi que os ângulos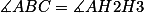 
. O problema é que eu não consegui provar que eles são iguais.
Rflbboy- Iniciante
- Mensagens : 8
Data de inscrição : 06/03/2013
Idade : 30
Localização : Brasil
Re: Geometria Plana
por Rflbboy Qua 10 Jul 2013, 14:03
Seja M o ponto médio do segmento BC, então
Se conseguir provar a igualdade desses ângulos o problema estará acabado!
Rflbboy- Iniciante
- Mensagens : 8
Data de inscrição : 06/03/2013
Idade : 30
Localização : Brasil
Re: Geometria Plana
por Rflbboy Qua 10 Jul 2013, 14:17
Eu vou postar todas as informações que consegui tirar da imagem, pois elas podem ajudá-los.
Os segmentos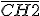
e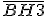 
são as alturas do 
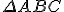, portanto, 
.
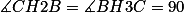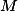é ponto médio do segmento 
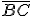e isso implica que 
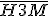é a mediana relativa à hipotenusa do 
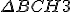e 
é 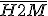a mediana relativa à hipotenusa do 
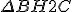. Portanto, 
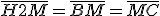e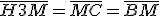 
.
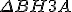é semelhante ao 
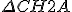(critério A.A.)
.
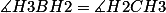é isósceles 
.
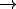
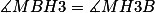O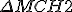
é isósceles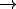 
.
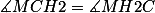O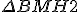
é isósceles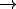 
.
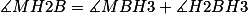O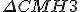
é isósceles 
.
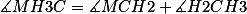Eu só consegui tirar essas informações da imagem!
Os segmentos
O
O
O
Eu só consegui tirar essas informações da imagem!
Rflbboy- Iniciante
- Mensagens : 8
Data de inscrição : 06/03/2013
Idade : 30
Localização : Brasil
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
