Aprendendo a derivar (1)

por **Euclides** Sáb 02 Fev 2013, 20:11

Vimos, no ítem 6 da exposição sobre limites, que um limite em particular originou, ou definiu, uma derivada. Essa derivada fornece a inclinação de uma reta tangente a uma curva em todos os pontos do domínio.

Ver: de um limite nasce uma derivada

Essa derivada é chamada "derivada primeira" porque pode ser derivada novamente originando derivadas de ordem superior como: derivada segunda, terceira, etc. Se notamos por $f'(x)$ a derivada primeira, analogamente faremos $f''(x),\;f'''(x)$ , etc para significar as derivadas de ordem superior.

Também é um bom momento para nos familiarizarmos com a notação introduzida pelo filósofo e matemático alemão Gottfried Leibnitz (Leipzig 1646 - Hanover 1716). Esta notação tem algumas particularidades que a tornam vantajosa em alguns aspectos do cálculo.

Definimos a inclinação de uma reta usando a notação

$\dpi{120} m=\frac{y-y_0}{x-x_0}=\frac{\Delta y}{\Delta x}$

de tal maneira que a inclinação da tangente é dada por uma derivada representada por

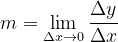
$\dpi{120} m=\lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x}$

Leibnitz usou a seguinte notação para escrever a mesma coisa:

$\dpi{120} m(x)=\frac{dy}{dx}$

significando a derivada de y em relação a x, onde fica explícito que y é uma variável dependente e x a variável independente. Essa notação tem a vantagem de criar dois operadores independentes que serão úteis futuramente.

Regras de derivação

Calcular uma derivada pela definição, isto é, pelo limite, nem sempre será tão simples. Felizmente foram desenvolvidas regras de derivação cuja aplicação facilitará enormemente as nossas vidas.

1. Derivada de uma constante

$\dpi{120} \boxed{f(x)=k\;\;\;\to\;\;\;f'(x)=0}$

2. Derivada de uma potência da variável

$\dpi{120} \boxed{f(x)=ax^n\;\;\;\to\;\;\;f'(x)=nax^{n-1}}$

3. Derivada da função polinomial

$\dpi{120} \\f(x)=a_1x^n+a_2x^{n-1}+...+a_{n-1}x+a_n\\\boxed{f'(x)=na_1x^{n-1}+(n-1)a_2x^{n-2}+..._1 }$

4. Derivada do produto

$\dpi{120} \boxed{f(x)=g(x).h(x)\;\;\to\;\;f'(x)=g'(x).h(x)+g(x).h'(x)}$

5. Derivada do quociente

$\dpi{120} \boxed{f(x)=\frac{g(x)}{h(x)}\;\;\;\to\;\;\;f'(x)=\frac{g'(x).h(x)-g(x).h'(x)}{\left [ h(x) \right ]^2}}$

6. Derivadas de funções exponenciais

$\dpi{120} \\\boxed{f(x)=a^{g(x)}\;\;\to\;\;f'(x)=a^{g(x)}.(\ln a).g'(x)}\\\boxed{f(x)=e^{g(x)}\;\;\;\to\;\;\;f'(x)=g'{x}.e^{g(x)}}$
7. Derivada do logarítimo

$\dpi{120} \\\boxed{f(x)=\log_a\left [g(x) \right ]\;\;\;\to\;\;\;f'(x)=\frac{g'(x)}{g(x)}\cdot\log_ae }\\\boxed{^{(*)}f(x)=\ln\left [g(x) \right ]\;\;\;\to\;\;\;f'(x)=\frac{g'(x)}{g(x)} }$

a regra marcada com um asterístico ^(*) será muito útil para o cálculo de várias outras derivadas. Vale a pena memorizar.

Voltaremos mais adiante com mais regras de derivação:

_________________________________

Para treinar, calcule as seguintes derivadas:

$\dpi{120} \\a)\;y=3x^{4}\;\;\;\;\;\;\;\;\;\;b)\;y=2x^3+4x-x+8\;\;\;\;\;\;\;\;\;\;c)\;y=(2x^3+4x).(3x^2-1)\\\\d)\;y=\frac{4x^5-2x}{3x^2}\;\;\;\;\;\;\;\;\;\;e)y=5^{2x+3}\;\;\;\;\;\;\;\;\;\;f)y=e^{4x^2-x+1}\\\\g)\;y=\sqrt{3x^2-4}\;\;\;\;\;\;\;\;\;\;h)\;y=(2x^2+2).\ln(4x^3)$
___________________________________

PS: se tiver dúvidas sobre a resolução de qualquer dos exercícios acima coloque sua dúvida como uma questão na seção Iniciação ao Cálculo.

Aprendendo a derivar (1)

Aprendendo a derivar (1)

Um fórum livre e democrático.