De um limite nasce a derivada (6)
2 participantes
Página 1 de 1
De um limite nasce a derivada (6)
por Euclides Sáb 02 Fev 2013, 14:39
Vamos aqui examinar um limite importante que nos ajudará a fazer uma travessia para um novo e poderoso domínio do cálculo: as derivadas.
O gráfico abaixo será nossa ferramenta:
Na figura 1 vemos a reta s, uma secante à uma curva dada (no caso uma função do terceiro grau) pelos pontos P e P'. É bastante fácil encontrar a inclinação dessa reta. Já sabemos que o seu coeficiente angular é dado por:
-f(x_0)}{x-x_0} "\dpi{120} m=\frac{f(x)-f(x_0)}{x-x_0}")
As figuras 1a e 1b mostram o comportamento de s quando o ponto P' se desloca sobre a curva, aproximando-se de P. Podemos ver que a secante vai se aproximando da tangente à curva no ponto P.
Você já deve ter percebido que esse raciocínio contém a ideia de limite. O comportamento da secante obedece a uma tendência enquanto
e no limite temos uma tangente. Em outras palavras, o coeficiente angular da reta tende ao coeficiente angular da tangente quando o que nos permite escrever
-f(x_0)}{x-x_0}} "\dpi{120} \boxed{m_t=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}}")
sendo "f(x)")
a função que descreve a curva e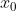 
o ponto no qual se deseja conhecer a inclinação da tangente. É evidente que isso nos permite encontrar a equação dessa tangente, já que temos o seu coeficiente angular e o ponto de tangência,  "\left (x_0,\;y_0 \right )")
.
Esta é a definição de derivada num ponto. A derivada de uma função em um ponto dado é o coeficiente angular da reta tangente à função nesse ponto.
\;\;\;ou\;\;\;m_t=\frac{df(x)}{dx}\;\;\;ou\;\;\;m_t=Df(x) "\dpi{120} m_t=f'(x)\;\;\;ou\;\;\;m_t=\frac{df(x)}{dx}\;\;\;ou\;\;\;m_t=Df(x)")
as tres formas de notação podem ser utilizadas significando todas a derivada de "f(x)")
.
Ou seja agora já sabemos como derivar uma função:
=\lim_{x\to&space;x_0}\frac{f(x)-f(x_0)}{x-x_0}} "\boxed{f'(x)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}}")
Importante: enquanto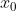 não está definido e, portanto é uma variável, a derivada ainda não possui um valor númerico e é uma função também.
Consideremos a função
=x^3 "\dpi{120} f(x)=x^3")
e vamos derivá-la de acordo com a definição de derivada
=\lim_{x\to x_0}\frac{x^3-x_0^3}{x-x_0}=\lim_{x\to x_0}\frac{(x-x_0)(x^2+xx_0+x_0^2)}{x-x_0} \\\\\\f'(x)=\lim_{x\to x_0}(x^2+xx_0+x_0^2)=3x_0^2 "\dpi{120} \\f'(x)=\lim_{x\to x_0}\frac{x^3-x_0^3}{x-x_0}=\lim_{x\to x_0}\frac{(x-x_0)(x^2+xx_0+x_0^2)}{x-x_0} \\\\\\f'(x)=\lim_{x\to x_0}(x^2+xx_0+x_0^2)=3x_0^2")
desde que ainda não atribuímos um valor para o ponto, temos ainda uma variável e a derivada é uma função dessa variável. Temos que
=x^3\;\;\;\to\;\;\;f'(x)=3x^2 "\dpi{120} f(x)=x^3\;\;\;\to\;\;\;f'(x)=3x^2")
essa função nos fornece a inclinação das tangentes ponto a ponto.
Aplicação:
encontre a equação da tangente à curva
no ponto  "(2,\;0)")
.
Uma exercício sobre limites:
-8}{x-1}=10\;\;\text{ calcule }\;\;\;\lim_{x\to 1}f(x) "\dpi{120} \\\text{se }\;\;\lim_{x\to 1}\frac{f(x)-8}{x-1}=10\;\;\text{ calcule }\;\;\;\lim_{x\to 1}f(x)")
Para encerrar esta etapa sobre limites, fica abaixo um link do fórum com mais de 200 exercícios resolvidos para você praticar:
Exercícios resolvidos - Limites
Espero que tenha valido a pena!
PS: coloque suas dúvidas como questões na seção Iniciação ao Cálculo
O gráfico abaixo será nossa ferramenta:
Na figura 1 vemos a reta s, uma secante à uma curva dada (no caso uma função do terceiro grau) pelos pontos P e P'. É bastante fácil encontrar a inclinação dessa reta. Já sabemos que o seu coeficiente angular é dado por:
As figuras 1a e 1b mostram o comportamento de s quando o ponto P' se desloca sobre a curva, aproximando-se de P. Podemos ver que a secante vai se aproximando da tangente à curva no ponto P.
Você já deve ter percebido que esse raciocínio contém a ideia de limite. O comportamento da secante obedece a uma tendência enquanto
sendo
Esta é a definição de derivada num ponto. A derivada de uma função em um ponto dado é o coeficiente angular da reta tangente à função nesse ponto.
as tres formas de notação podem ser utilizadas significando todas a derivada de
Ou seja agora já sabemos como derivar uma função:
Importante: enquanto
Consideremos a função
e vamos derivá-la de acordo com a definição de derivada
desde que ainda não atribuímos um valor para o ponto, temos ainda uma variável e a derivada é uma função dessa variável. Temos que
essa função nos fornece a inclinação das tangentes ponto a ponto.
Aplicação:
encontre a equação da tangente à curva
- Solução:
a reta será
que passa pelo ponto (2, 0), ou seja:
Uma exercício sobre limites:
- Solução:
Para encerrar esta etapa sobre limites, fica abaixo um link do fórum com mais de 200 exercícios resolvidos para você praticar:
Exercícios resolvidos - Limites
Espero que tenha valido a pena!
PS: coloque suas dúvidas como questões na seção Iniciação ao Cálculo
Última edição por Euclides em Sex 05 Abr 2013, 14:49, editado 3 vez(es)
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.
Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.
Euclides- Fundador
- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
Iago6- Fera
- Mensagens : 808
Data de inscrição : 19/12/2011
Idade : 31
Localização : Natal
Tópicos semelhantes» Limite sem derivada
» Limite sem derivada 2
» Limite e derivada
» Derivada e limite
» Limite e Derivada
» Limite sem derivada 2
» Limite e derivada
» Derivada e limite
» Limite e Derivada
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
