Comprimento do arco
3 participantes
Página 1 de 1

Maluco Beleza- Iniciante
- Mensagens : 33
Data de inscrição : 08/02/2012
Idade : 49
Localização : Eldorado - MT
rihan- Estrela Dourada

- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
 Re: Comprimento do arco
Re: Comprimento do arco
Olá Mestre.
Pode-se chegar a um resultado numérico disso?
Agradecido...
Pode-se chegar a um resultado numérico disso?
Agradecido...

Maluco Beleza- Iniciante
- Mensagens : 33
Data de inscrição : 08/02/2012
Idade : 49
Localização : Eldorado - MT
 Re: Comprimento do arco
Re: Comprimento do arco
Nas minhas contas que eu fiz deu: 0 (zero)
Mas...tenho dúvidas.
Mas...tenho dúvidas.

Maluco Beleza- Iniciante
- Mensagens : 33
Data de inscrição : 08/02/2012
Idade : 49
Localização : Eldorado - MT
 Re: Comprimento do arco
Re: Comprimento do arco
Dúvidas você não pode ter.
Está errado.
Se você pensar na fórmula ou esboçar a função vai ver que não pode dar zero:
s = ∫√( 1 + [f'(x)]² ).dx
Nunca vai dar zero se os limites inferior e superior forem diferentes, e são: ∏/4 e 3∏/4
Graficamente:

O resultado é ≈ 6,1822
Caso você não saiba derivar e integrar, não vai acertar...
Aí, a sua dúvida não seria a questão de calcular o comprimento, que é somente uma fórmula, mas de saber derivar e integrar...
E, nesse caso, é uma integral cabeluda ...
Muito trabalho... Haja conta !
Está errado.
Se você pensar na fórmula ou esboçar a função vai ver que não pode dar zero:
s = ∫√( 1 + [f'(x)]² ).dx
Nunca vai dar zero se os limites inferior e superior forem diferentes, e são: ∏/4 e 3∏/4
Graficamente:
O resultado é ≈ 6,1822
Caso você não saiba derivar e integrar, não vai acertar...
Aí, a sua dúvida não seria a questão de calcular o comprimento, que é somente uma fórmula, mas de saber derivar e integrar...
E, nesse caso, é uma integral cabeluda ...
Muito trabalho... Haja conta !
rihan- Estrela Dourada

- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil

Man Utd- Grupo
Velhos amigos do Fórum
- Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
 Re: Comprimento do arco
Re: Comprimento do arco
Olá 
 !
!
Na verdade, a solução do Man Utd está incorreta.
O suficiente para o aprendizado foi fornecido para quem postou a questão:

Acredito que esse fórum não é para resolver listas de exercícios de Cálculo I e II de estudantes universitários, ainda mais para os que não sabem e não querem saber derivar ou integrar. Esse foi o motivo d'eu não detalhar a solução da questão
Man Utd forneceu o link da sua fonte, que mostra a fórmula:
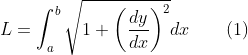
Que foi a por mim fornecida, trocando-se L por s e r por y (ou f ), obviamente...
Parametrizando-se em θ :
y = g(θ)
x = h(θ)
Obtendo-se:


Fazer a parametrização de uma função circular (cossecante) é, no mínimo, muito estranho...
Tipo trocar seis por meia dúzia...
Mas, vamos lá...
Resolvendo-se:
x = h(θ)
x = θ
dx/dθ = 1
y = g(θ)
y = - 7 csc(θ)
dy/dθ = - 7 csc(θ) cot(θ)
(dy/dθ)² = 49 csc²(θ) cot²(θ)
Usando-se a fórmula para os limites de θ variando de ∏/4 até 3∏/4 :
L = ∫ √( (dx/dθ)² + (dy/dθ)² ) dx
L = ∫ √( 1 + 49 csc²(θ) cot²(θ) ) dx
Sabendo-se a identidade:
csc²(θ) ≡ 1 + cot²(θ)
Tem-se:
L = ∫ √( 1 + 49(1 + cot²(θ) ) cot²(θ) ) dx
L = ∫ √( 1 + 49( cot²(θ) + cot4(θ) ) dx
Resolvendo-se, numericamente:
L ≈ 6,1822
Uma tristeza visitar o fórum e ver que as mesmas coisas das quais sempre discordei, discordo e discordarei , continuem acontecendo...
OBS: Ressaltei em vermelho onde foi o erro do monitor.
Na verdade, a solução do Man Utd está incorreta.
O suficiente para o aprendizado foi fornecido para quem postou a questão:

Acredito que esse fórum não é para resolver listas de exercícios de Cálculo I e II de estudantes universitários, ainda mais para os que não sabem e não querem saber derivar ou integrar. Esse foi o motivo d'eu não detalhar a solução da questão
Man Utd forneceu o link da sua fonte, que mostra a fórmula:
Que foi a por mim fornecida, trocando-se L por s e r por y (ou f ), obviamente...
Parametrizando-se em θ :
y = g(θ)
x = h(θ)
Obtendo-se:
Fazer a parametrização de uma função circular (cossecante) é, no mínimo, muito estranho...
Tipo trocar seis por meia dúzia...
Mas, vamos lá...
Resolvendo-se:
x = h(θ)
x = θ
dx/dθ = 1
y = g(θ)
y = - 7 csc(θ)
dy/dθ = - 7 csc(θ) cot(θ)
(dy/dθ)² = 49 csc²(θ) cot²(θ)
Usando-se a fórmula para os limites de θ variando de ∏/4 até 3∏/4 :
L = ∫ √( (dx/dθ)² + (dy/dθ)² ) dx
L = ∫ √( 1 + 49 csc²(θ) cot²(θ) ) dx
Sabendo-se a identidade:
csc²(θ) ≡ 1 + cot²(θ)
Tem-se:
L = ∫ √( 1 + 49(1 + cot²(θ) ) cot²(θ) ) dx
L = ∫ √( 1 + 49( cot²(θ) + cot4(θ) ) dx
Resolvendo-se, numericamente:
L ≈ 6,1822
Uma tristeza visitar o fórum e ver que as mesmas coisas das quais sempre discordei, discordo e discordarei , continuem acontecendo...
OBS: Ressaltei em vermelho onde foi o erro do monitor.
rihan- Estrela Dourada

- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
 Re: Comprimento do arco
Re: Comprimento do arco
rihan escreveu:Olá
!
Na verdade, a solução do Man Utd está incorreta.
O suficiente para o aprendizado foi fornecido para quem postou a questão:
Acredito que esse fórum não é para resolver listas de exercícios de Cálculo I e II de estudantes universitários, ainda mais para os que não sabem e não querem saber derivar ou integrar. Esse foi o motivo d'eu não detalhar a solução da questão
Man Utd forneceu o link da sua fonte, que mostra a fórmula:
Que foi a por mim fornecida, trocando-se L por s e r por y (ou f ), obviamente...
Parametrizando-se em θ :
y = g(θ)
x = h(θ)
Obtendo-se:
Fazer a parametrização de uma função circular (cossecante) é, no mínimo, muito estranho...
Tipo trocar seis por meia dúzia...
Mas, vamos lá...
Resolvendo-se:
x = h(θ)
x = θ
dx/dθ = 1
y = g(θ)
y = - 7 csc(θ)
dy/dθ = - 7 csc(θ) cot(θ)
(dy/dθ)² = 49 csc²(θ) cot²(θ)
Usando-se a fórmula para os limites de θ variando de ∏/4 até 3∏/4 :
L = ∫ √( (dx/dθ)² + (dy/dθ)² ) dx
L = ∫ √( 1 + 49 csc²(θ) cot²(θ) ) dx
Sabendo-se a identidade:
csc²(θ) ≡ 1 + cot²(θ)
Tem-se:
L = ∫ √( 1 + 49(1 + cot²(θ) ) cot²(θ) ) dx
L = ∫ √( 1 + 49( cot²(θ) + cot4(θ) ) dx
Resolvendo-se, numericamente:
L ≈ 6,1822
Uma tristeza visitar o fórum e ver que as mesmas coisas das quais sempre discordei, discordo e discordarei , continuem acontecendo...
OBS: Ressaltei em vermelho onde foi o erro do monitor.
Olá
Mestre Rihan, eu não parametrizei o que fiz foi utilizar a fórmula
Abraço.

Man Utd- Grupo
Velhos amigos do Fórum
- Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
 Re: Comprimento do arco
Re: Comprimento do arco
Sim Man Utd,
O problema é que você não compreendeu o espírito da coisa...
Quem postou, como a grande maioria nesse fórum, não postou o texto original, fornecendo origem ou autoria.
Este fato, repetitivo, foi inúmeras vezes alertado por mim ao Euclides, mas, pelo visto, continua se repetindo e nada se alterou nesses quase 3 anos.
Vou esclarecer para você:
Aonde está ESCRITO que a curva está na forma POLAR ?!?
Quem postou achou que qualquer um assim iria adivinhar e, preguiçosamente, não copiou a questão verbatim !
Insisti, inutilmente, chegando a mostrar a curva que entendi que era...
Mas, como desconfiava, o autor não se manifestou, sequer percebeu.
Ter "r" e "teta" ou "s" e "t" ou "L" e "p" não significa que está na forma polar !!!
Se assim fosse, e sei e sempre soube que o é, não era problema de Iniciação ao Cálculo !!!!
Vamos ver, sabendo ser em coordenadas polares:
r = -7 csc(θ)
x = r cos(θ) = -7 csc(θ) cos(θ) = -7 cos(θ) / sen(θ) = -7 cot(θ)
y = r sen(θ) = -7 csc(θ) sen(θ) = -7 sen(θ) / sen(θ) = -7
Variando-se θ de ∏/4 até 3∏/4 :
cot(∏/4) = 1
cot(3∏/4) = -1
De 1 até -1 são -2, vezes -7 dá 14 u.c.
Nada de cálculo...
A "curva" é um segmento de reta de comprimento 2, paralelo ao eixo X e abaixo dele 7 u.c.
Por isso, disse ao postador que bastava esboçar a curva...
Saudações polares.
O problema é que você não compreendeu o espírito da coisa...
Quem postou, como a grande maioria nesse fórum, não postou o texto original, fornecendo origem ou autoria.
Este fato, repetitivo, foi inúmeras vezes alertado por mim ao Euclides, mas, pelo visto, continua se repetindo e nada se alterou nesses quase 3 anos.
Vou esclarecer para você:
Aonde está ESCRITO que a curva está na forma POLAR ?!?
Quem postou achou que qualquer um assim iria adivinhar e, preguiçosamente, não copiou a questão verbatim !
Insisti, inutilmente, chegando a mostrar a curva que entendi que era...
Mas, como desconfiava, o autor não se manifestou, sequer percebeu.
Ter "r" e "teta" ou "s" e "t" ou "L" e "p" não significa que está na forma polar !!!
Se assim fosse, e sei e sempre soube que o é, não era problema de Iniciação ao Cálculo !!!!
Vamos ver, sabendo ser em coordenadas polares:
r = -7 csc(θ)
x = r cos(θ) = -7 csc(θ) cos(θ) = -7 cos(θ) / sen(θ) = -7 cot(θ)
y = r sen(θ) = -7 csc(θ) sen(θ) = -7 sen(θ) / sen(θ) = -7
Variando-se θ de ∏/4 até 3∏/4 :
cot(∏/4) = 1
cot(3∏/4) = -1
De 1 até -1 são -2, vezes -7 dá 14 u.c.
Nada de cálculo...
A "curva" é um segmento de reta de comprimento 2, paralelo ao eixo X e abaixo dele 7 u.c.
Por isso, disse ao postador que bastava esboçar a curva...
Saudações polares.
rihan- Estrela Dourada

- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Comprimento de um arco
» Comprimento do Arco
» Comprimento do arco
» Comprimento de arco
» Comprimento de Arco
» Comprimento do Arco
» Comprimento do arco
» Comprimento de arco
» Comprimento de Arco
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












