(PUC) Determinação do centro e do raio.

(PUC) Quantos são os pontos que têm coordenadas inteiras e são interiores á circunferencia de equação x² + y² = 6
a)9
b) 13
c) 18
d) 21
e) 25

Gabarito

Spoiler:

--
Achei
C (0;0) r = V6, porém não sei qual raciocínio usar para resolver esse problema

O raciocínio que eu usei foi o seguinte:

A distancia entre os pontos procurados e o centro deve ser menor do que o valor do raio,pois assim os pontos pertenceram a circunferencia.

Como o centro vale (0;0)




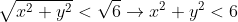
teremos como solução

x=+-2------>y=+-1

x=+-1------>y=+-2

x=+-1------->y=+-1

x=+-2------->y=0

x=+-1------->y=0

......

Contando teremos 21.

PS:não sei se tem um modo mais facil de saber quantas são as solucoes,eu contei de uma em uma.

É, realmente chega ao resultando, mas imagino que haja uma formula para resolução desse tipo de questão, andei pesquisando e não achei nada.

Entretanto obrigado por ajudar, até.

Sim,acho que deve haver outro modo,pois se tivessemos um raio maior ficaria meio inviavel resolver do jeito que fiz.Caso vc encontre outro meio de resolver poste aki oks

De nada!

Não teremos uma "fórmula" , mas um jeito mais fácil de resolver ,caso o raio fosse muito maior , seria usar COMBINATÓRIA. Vamos lá!
Sabemos que o raio vale raiz quadrada de 6, que é aproximadamente igual a 2,5
.Teremos então em Y um "máximo" de 2,5 e um "mínimo" de -2,5 , para x é a mesma coisa, já que o raio é constante em toda a circunferência.
Entre 2,5 e -2,5 temos 5 números inteiros, a saber, 2, 1, 0, -1 e -2.
Um ponto no plano cartesiano é um par ordenado (x;y)
A pergunta é: Quantos pares ordenados nós conseguiremos formar com os números 2,1,0,-1 e -2?
Vamos pensar sem o zero primeiro:
poderíamos colocar 4 números no x e 4 números no y, o que nos daria 16 pares.
Agora com o zero:
temos apenas um número no x e 5 possibilidades no y(conta-se o zero como possibilidade, já que o par (0;0) é válido), isso nos dá 5 pares.
Temos um total de 16+5 pares, o que nos dá o gabarito!

Usando da ferramenta do Princípio da Multiplicação da Combinatória, poderíamos facilmente descobrir quantos pontos(com coordenadas inteiras) teríamos em uma circunferência de raio R.