[Energia e Trabalho] Dúvida teórica

Fala, pessoa! Tudo bem?

Então, estou com uma dúvida teórica que está me matando! A dúvida é a seguinte:
Ontem, estudando "Princípio da Trajetória Alternativa", eu pensei em demonstrar esse princípio e me perdi na demonstração. Depois, percebi que poderia demonstrar o princípio apenas demonstrando que o trabalho independe do espaço percorrido, mas sim do deslocamento.

Aí que está minha dúvida, por que o trabalho não depende do espaço percorrido?
Uma vez que a demonstração da fórmula de trabalho a partir da fórmula de energia cinética associa, justamente, o espaço percorrido em vez do deslocamento.

Onde estou errado? Poderiam provar que o trabalho independe do espaço percorrido?

O trabalho de uma força constante é definido como:

Trabalho é o produto interno ou escalar entre o vetor força e o vetor deslocamento. Matematicamente:



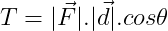
sendo o menor ângulo entre os dois vetores.

Isso não deve ser confundido com trabalho realizado por, ou sobre um campo conservativo. Nesse caso, o trabalho dependerá apenas do vetor deslocamento medido sobre a direção das linhas de força do campo, ou seja, dependerá apenas da posição inicial e da posição final.

Os princípios da Física são muito simples e intuitivos.

Percebemos uma coisa na Natureza: se deixarmos uma coisa quieta ela fica quieta.

Pode parecer idiota, mas não o é.

Dessa aparente bobagem intuimos, induzimos, concluimos e verificamos rotineiramente que: para alterarmos o estado de uma coisa — entendendo-se por estado as coordenadas (x,y,z,t) da coisa — se faz necessário a interação dessa coisa com outra coisa ou, dependendo do gosto do observador, da outra coisa com a coisa. Como é interação, termo que exige explicitamente reciprocidade, tanto faz.

Da observação do cotidiano também surge outra coisinha bem simples: é diferente você receber uma pedrada com uma pequena pedra atirada devagar e a mesma pedra atirada mais rapidamente.

Ao ficar sendo apedrejado, o valente observador da Natureza percebe também mais outras coisas:

Quanto mais matéria tiver a pedra, maior é o baque, mantendo-se a mesma rapidez.

Quanto mais frontal for o choque, mais estrago faz. Logo, este martirizante experimento em favor do conhecimento também depende da direção, da trajetória, do ângulo de ação.

A essa coisa percebida, que cada coisa em movimento "carrega" em si, foi dado o nome de momentum.

Sendo diretamente proporcional à massa e à rapidez, ela é proporcional ao produto dessas grandezas.

Poderíamos definí-la assim:

p ≡ m.v

Mas estaríamos omitindo algo importante: a direção !

Atualmente, podemos representá-la de uma forma sintética e elegante, graças às cabeças de geniais Físicos e Matemáticos, que introduziram a noção de grandezas vetoriais e os respectivos representantes: os vetores.

Sem esquecer de nada de nossas observações, agora sim a definimos corretamente, trocando a escalar rapidez pelo vetor velocidade "v":

p ≡ m.v

Beleza. O vetor momentum p tema mesma direção (e sentido, como gostam de complicar os lusófonos) que o vetor v, já que a grandeza escalar massa é sempre positiva.

O mais geral e universal e único princípio que é necessário para desenvolver toda a Mecânica Newtoniana e Galileniana é o da conservação do momentum (que no Brasil e Portugal é chamado de quantidade de movimento ou momento linear).

Em sua forma mais simples, ele nos diz que:

Se duas partículas estiverem sujeitas somente às suas interações (mútuas, obviamente e pleonasticamente), o momentum total permanece constante (no tempo, claro e pleonasticamente também).

Sendo o momentum total P a soma vetorial dos momenta:

P(t) = p₁(t) + p₂(t)

A tradução simbólica para o matematiquês é:

p₁ + p₂ = p'₁ + p'₂ = ... = P

Onde a linha (') representa um outro instante qualquer.

Poderíamos complicar a notação assim:

p₁(t₁) + p₂(t₁) = p₁(t₂) + p₂(t₂) = ... = P

Onde P é um vetor constante, independente do tempo.

Mas, por simplicidade e facilidade, vamos manter as linhas (')...

Esse simplíssimo princípio, desde então, não foi descumprido em qualquer observação feita pela comunidade científica, mantendo-se verdadeiro e intocável até agora.

Mesmo para velocidades relativísticas altíssimas e próximas da velocidade da luz, onde se faz necessário uma correção para a massa, o princípio continua válido.

E, espantosamente para a maioria, até mesmo para quando não há massa, quando entramos no universo oscilatório das ondas eletromagnéticas, ele continua válido !

O Princípio é naturalmente estendido para um sistema com mais de duas partículas:

O momentum total de um sistema isolado de partículas é constante.

Entendendo-se "sistema isolado" como sendo um sistema onde as interações são devidas exclusivamente e somente às partículas que o compõe.

Em outras palavras, não há agentes externos interagindo com o sistema isolado.

De uma forma mais realística e crítica, até pode existir interações externas, mas seus valores são desprezíveis, em ordem de grandeza, quando comparados com os valores das interações entre as partículas do sistema.

Vamos reler e analisar todas as implicações deste fantástico e simples Princípio:

1) Para haver mudança no momentum de uma partícula isolada é necessária uma interação.

2) Caso não haja essa interação, o momentum do sistema permanece constante :face:.

3) O momentum do sistema está relacionado à massa e a velocidade, se ele se mantiver constante, em sendo uma grandeza vetorial, somente duas hipóteses podem ocorrer:

(i) Ou ele está em repouso (v = 0)

(ii) Ou são constantes sua massa e a velocidade vetorial e, nesse caso, para que o vetor velocidade seja constante, obrigatoriamente o sistema estará em movimento, no qual o módulo e a direção da velocidade não variam, movimento este que tem que ter uma trajetória retilínea e velocidade uniforme, denominado de "movimento retilíneo uniforme" (MRU).

4) Vamos colocar outra partícula no nosso sistema. Se houver variação do momentum da primeira partícula, houve uma interação com a outra partícúla recém-chegada.

Mas, pelo nosso belo princípio, o momentum total TEM QUE permanecer constante !

Matematicamente:

p₁ + p₂ = p'₁ + p'₂

ou:

p'₁ + p'₂ = p₁ + p₂

ou:

p'₁ - p₁ = p₂ - p'₂

ou:

∆p₁ = - ∆p₂

Voltando a nossa linguagem: a variação do momentum de uma partícula é o simétrico ou oposto da variação da outra.

Se dividirmos ambas variações por um intervalo de tempo "∆t", teremos:

∆p₁ / ∆t = - ∆p₂ / ∆t

Essa razão ou taxa de variação média do momentum em relação ao tempo recebeu um nome mais simples: Força Média.

Se formos diminuindo progressivamente o intervalo "∆t" para algo infinitesimal, representamos matematicamente e mais sinteticamente assim:

dp₁ / dt = - dp₂ / dt

A essa razão infinitesimal, que nos dá a "velocidade" da variação do momentum a cada instante, apelidamos, para simplificar, de FORÇA INSTANTÂNEA, ou, mais simples, o vetor FORÇA.

F₁₂ = - F₂₁

A força que '1' "exerce" em "2" é simétrica (oposta) à força que '2' "exerce" em '1'.

Força, então, é simplesmente mais um constructo do ser humano, somente um conceito, um nome para uma taxa instantânea, somente uma simplificação para as nossas mentes, somente uma "materialização", uma "personificação" de um ente, o ente que "faz" a ação...

Se as massas das partículas se mantiverem constantes, teremos, matematicamente:

F = ∆p / ∆t = ∆m.v / ∆t = m.∆v / ∆t

Como a aceleração vetorial média a é definida por

a ≡ ∆v / ∆t

Tem-se:

F = m.a

Fazendo "∆t" um infinitésimo, ter-se-á, analogamente, para "m" constante:

F = dp/dt = d(m.v) / dt = m . dv/dt

Como a aceleração vetorial instantânea a é definida por

a ≡ dv / dt

Então:

F = m.a

Que nos diz que, quando a massa é constante a FORÇA em cada instante pode ser calculada pelo produto "m.a".

Pela definição de FORÇA:

F ≡ dp/dt

Então:

dp = F.dt

Caso a força F seja constante (vetorialmente !):

∆p = F.∆t

E apelidamos:

F.∆t := IMPULSO

Lemos assim:

A variação do momentum de uma partícula sujeita a uma força constante, num intervalo de tempo, pode ser calculada pelo IMPULSO DA FORÇA F constante:F.∆t.

Vamos a um exemplo:Se você deixar uma bola de 1 kg cair de uma altura de 5 m, sujeita somente à ação gravitacional da terra, com |g| de 10 m/s² e, ao bater no chão, ela quicar e subir 4 m, qual seria o impulsoda força gravitacional durante a queda e qual o impulso recebido pela força de contato com o chão ?

Pela Cinemática:

m = 1

vo = 0

h = 5

g = 10

po = m.vo = 1.0 = 0

v₁² = vo² + 2g.h

v₁ = √(2g.h)

v₁ = √(2.10.5) = √(10.10)

v₁ = ±10

Vamos considerar o referencial comum, "positivo para cima", então:

v₁ = -10 m/s

∆p = m.v₁ - m.vo

∆p = 1.(-10) - 0

∆p = - 10 kg.m/s


Pelo Impulso:

Sendo a aceleração da gravidade constante, a força peso também o é . Então, podemos usar o "Impulso" para calculara variação do momentum.

∆p = F.∆t

Precisamos calcular o "∆t" pela cinemática:

to = 0

v₁ = vo + g.∆t

∆t = v₁ / g

∆t = -10 /-10

∆t = 1 s

Logo:

∆p = F.∆t = m.g.∆t = 1.(-10).1

∆p = - 10 kg.m/s

Agora vamos calcular o impulso dado pela força de contato com o chão.

Não sabemos nada sobre a força, sua função em relação ao tempo.

Menos ainda sobre o tempo que ela agiu. Medir esse tempo, o tempo de contato com o chão, é complicado, às vezes impraticável...

Vamos fazer o que nos resta, vamos calcular o impulso pela variação do momentum, nossa única possibilidade.

Antes do choque a velocidade era -10 m/s.

Precisamos saber qual a velocidade após o choque, após a interação do chão com a partícula, após a ação da força de contato.

Vamos do fim para o início. Sabemos que a bola subiu a 4 m, quando zerou sua velocidade, então:

v₃² = v₂² - 2g.h

0 = v₂² - 2.10.4

v₂² = 2.10.4

v₂ = √(2.10.4)

v₂ = √(80)

v₂ ≈ 9 m/s

Finalmente:

p₂ - p₁ = m.v₂ - m.v₁

p₂ - p₁ = 1.9 - (-10)

p₂ - p₁ = 19 kg.m/s

Caso conseguíssemos medir o tempo de ação da força de contato com o chão, poderíamos calcular a força média, que, antecipadamente, sabemos ser muito grande, pois sabemos que o tempo de contato é muito pequeno.

O que Newton então fez, foi metodificar e matematizar esse conhecimento.

Você, seguramente pode identificar todas as 3 "Leis de Newton" na análise que fizemos.

Infelizmente, com o passar do tempo, os físicos tentando "simplificar"
para os seus discentes, complicaram algumas coisas, no meu entender.

Por outro lado, felizmente, simplificaram certas coisas ao criarem
outros conceitos importantes, práticos e necessários para simplificarem
as calculeiras vetoriais: os conceitos de TRABALHO e ENERGIA, duas grandezas escalares.

>>> Continua >>>

>>> Continuação >>>

Bem, se tivermos a força constante, tudo bem.

Mas, e se não for ?

O gigante Newton também se fez essa pergunta e, para resolvê-la, teve que inventar uma matemática nova, o Cálculo Infinitesimal, os conceitos de derivadas, diferenciais e integrais. Juntamente com um outro gigante, Leibnitz, se tornaram os pais do Cálculo Diferencial e Integral.

Ao representarmos graficamente uma força que é constante no tempo, obteremos o seguinte:




O produto (F.∆t) é equivalente à área da figura. A área então representa o Impulso "fornecido" pela força durante o tempo ∆t.

Quando temos F variando no tempo, calculamos também a área da figura, fazendo uma soma de áreas (impulsos) infinitesimais, dizemos que integramos a função:

Impulsos Infinitesimais: dI = F.dt

Soma: ∑(dI) = ∑(F.dt)

Matematicamente trocamos o "S" grego da soma (∑: sigma) por um "S" mais estiloso, simbolizando a integral:

∫dI = ∫ F.dt

I = ∫ F.dt

O que nada mais é que a área subtendida pela curva da função e o intervalo de tempo considerado:




Menos um problema !

Mas temos outros !

Quase nunca temos F em função do tempo !!!

Geralmente temos F como função da posição r(x, y, z) ...

Os físicos e matemáticos então criaram uma nova entidade, um novo conceito para resolver esse impasse e facilitar os cálculos e o os experimentos: o TRABALHO, W  (de work, em inglês).

Seja uma força F, função da posição r(x,y,z), agindo durante um intervalo de tempo ∆t numa partícula que descreve uma trajetória C qualquer.

O trabalho infinitesimal da uma força é dado pelo produto escalar entre o vetor Força e o vetor deslocamento infinitesimal ocorrido num intervalo de tempo também infinitesimal :

dW = F.dr

Pela definição de produto escalar:

dW = |F|.|dr|.cos(θ)

Ou, mais simples:

dW = F.ds.cos(θ)

Onde "ds" é um deslocamento infinitesimal e "θ" o ângulo entre os vetores força F e deslocamento dr.

Podemos pensar em "F.cos(θ)" como a componente da força na direção do movimento, componente tangente à trajetória:

Ft = F.cos(θ)

Portanto:

dW = Ft.ds




Para obtermos o trabalho integral durante o deslocamento na trajetória durante o intervalo de tempo ∆t , basta procedermos da mesma forma que fizemos com o impulso:

W = ∑(dW) = ∑(F.dr)

W = ∑(F.dr)

W = ∑(Ft.ds)

Se  F (e, logicamente, Ft) for constante:

W = Ft . ∑(ds)

W = Ft . ∆s

Caso não seja, fazemos da mesma forma como fizemos para o Impulso:

W =  ∫Ft.ds

Que também é a área sob a curva da função F(s) e o eixo do espaço percorrido ou deslocamento no intervalo de tempo considerado:



Para quem já faz Iniciação ao Cálculo, que, na minha visão, deveria se dado a partir do 2° ano do ciclo médio, não há a necessidade de se usar a área do gráfico. Existe uma "taboada" para se calcular derivadas e suas inversas, as integrais:

A derivada de uma soma é a soma das derivadas. A integral de uma soma é a soma das integrais:

y = u(x) + v(x) --> dy/dx = y' = u'+ v' --> ∫(u+v).dx = ∫u.dx + ∫v.dx

A derivada de y = constante é zero, a integral de zero é uma constante.

y = C --> dy/dx = y' = 0 --> ∫0.dx = C

A derivada de y = x é 1, a integral de 1 é x mais uma  constante.

y = x --> dy/dx = y' = 1 -->∫(1+0).dx = ∫1.dx + ∫0.dx  = x + C

A derivada de y = x² é 2x, a integral de 2x é x² mais uma  constante.

y = x² --> dy/dx = y' = 2x -->∫2x.dx = x² + C

A derivada de y = xⁿ é n.xⁿˉ¹ , a integral de n.xⁿˉ¹  é  xⁿ  mais uma  constante.

y = xⁿ --> y' = n.xⁿˉ¹ --> ∫n.xⁿˉ¹.dx = xⁿ + C

Mais umas:

y = sen(x) --> y' = cos(x)

y = ln(x) --> y' = 1/x

y = u(x) . v(x) --> y' = u'.v + u.v'

y = u(x) / v(x) --> y' = (u'.v - u.v')/v²

E a regra da cadeia:

y(u(x)) --> dy/dx = (dy/du ) . (du/dx)

Exemplo dela:

y = sen(ln(x)) -->

dy/du = cos(ln(x))

du/dx = 1/x

dy/dx = y' =  cos(ln(x)) .(1/x) = cos(ln(x))/x

E aí vai.

Agora vamos a uma aplicação interessante desses novos conhecimentos...

A Lei de Hook para molas nos diz que:

F = -k.∆x

F = -k.(x - xo)

Se considerarmos a posição inicial da mola como zero e como sendo a posição natural e estável da mola, teremos:

F = -k.x

Fica mais simples.

Se quisermos saber o trabalho realizado pela força elástica durante um deslocamento x , ao comprimirmos a mola:

Podemos graficar a força e calcular a área facilmente, ou, para exemplificar, podemos usar nossos conhecimentos de derivadas e integrais:

W = ∫F.dx

W = ∫(-k.x).dx = -k∫x.dx = k∫(2x/2).dx =(k/2)∫2x.dx = -(k/2).x² + C

Para descobrirmos a constante C, fazemos, por exemplo, x = 0, isto é, trabalho nulo, pois não houve deslocamento:

W = 0 + C = 0 --> C = 0

Prontinho:

Trabalho da Força Elástica:

W = - k.x²/2

O negativo indica que a força estava sempre oposta ao deslocamento.

Agora vamos criar outra entidade.

Nossa fórmula nos diz:

W =  ∫Ft.ds

Vamos calcular o trabalho realizado por uma força qualquer agindo durante o deslocamento de uma partícula entre instantes "1" e "2" quaisquer.
Como:

Ft = m.a

E:

a ≡ dv/dt

E:

v ≡ ds/dt --> ds = v.dt

Temos:

W = ∫m.(dv/dt)(v.dt)

W = ∫m.v.dv

W = m∫v.dv

W = m.v²/2 + C    

Para t = t₁ --> v = v₁ , temos trabalho nulo, pois não houve deslocamento ainda:

m.v₁²/2 + C = 0

C =  - m.v₁²/2

Para t = t₂ --> v = v₂

W = m.v₂²/2 + C

W = m.v₂²/2 - m.v₁²/2

Resultado IMPORTANTÍSSIMO !

Tão importante e notável que essa quantidade ganha um nome especial:

ENERGIA CINÉTICA :=    m.v²/2

ou m.v.v/2 =  p.v/2

Ec ≡ m.v²/2 = p.v/2

O que acarreta o Teorema Do Trabalho:

O tabalho da resultante das forças agindo sobre um corpo durante dois instantes quaisquer é igual a variação de energia cinética desse corpo durante este intervalo de tempo.

W = ∆Ec

Importantíssimo reparar que o trabalho só depende da energia cinética inicial e da final.

Vamos ver agora um caso comum, cotidiano, o trabalho da força peso ao abandonarmos uma partícula de massa m sob a ação da gravidade constante g entre dois instantes quaisquer.

Se a aceleração é constante e a massa também, então a força é constante e chamada de peso da partícula. Teremos:


W = F.∆y

W = m.(-g)(y₂ - y₁)

W = m.g.(y₁ - y₂)

W = m.g.y₁ - m.g.y₂

A esse termo notável, que ocorre também freqüentemente, denominamos:

ENERGIA POTENCIAL (GRAVITACIONAL).


Ep ≡ m.g.y + C

Onde C é uma constante arbitrária, escolhida conforme o caso. Em se tratando de queda de energia potencial gravitacional em ocais p´roximos da superfície da Terra, escolhemos C = 0 para y = 0 (nível do solo). Quando, diferentemente, tratamos de satélites ou planetas, escolhemos C = 0 para y = ∞.

Como nos nossos cálculos vamos fazer uso da diferença entre energias potenciais, a constante vai desaparecer.

Poderíamos também calcular o trabalho pela variação de energia cinética:

W = ∆Ec = m.v₂²/2 - m.v₁²/2

E escrever, para este caso:

W = ∆Ec = - ∆Ep

Quando podemos escrtever isto, dizemos que a força é conservativa, ou que o campo gravitacional é conservativo.

Uma força (ou campo) é conservativa quando o trabalho pode ser expresso pela variação de sua energia potencial.

Quando isso ocorre, o trabalho independe da trajetória, só dependendo do estados inicial e final da energia potencial.

Nesses casos conservativos podemos escrever:

∆Ec = - ∆Ep

Ec' - Ec = Ep - Ep'

Ec' + Ep' = Ec + Ep = E = constante

Onde:

E := Energia Mecânica Total da Partícula

E então enunciarmos o Princípio da Conservação da Energia Mecânica Total:

Em campos conservativos a energia total de um sistema se mantém constante.

Finalmente vamos definir uma grandeza útil: a POTÊNCIA INSTANTÂNEA.

Ela nada mais é do que a taxa de variação instantânea do trabalho no tempo, isto é, o trabalho infinitesimal fornecido ou recebido a cada variação infinitesimal do tempo:


P ≡ dW/dt

Como:

dW = F.dr

P = F.dr/dt

P = F.v

Sua unidade no SI é o Watt (lê-se "uat"): W = J/s

É isso, por enquanto.

Saudações potenciais !

Caso queira se aprofundar mais, aconselho a leitura do excelente livro "Fundamental University Physics", do Marcelo Alonso e Edward Finn. Lá está muito melhor explicado o que resumi aqui.

Ele existe também em português (razoável tradução feita por equipe da USP) e em espanhol...

Obrigado, mestres Euclides e rihan!

Como sempre, palavras muito sábias e esclarecedoras do mestre rihan.
Muitíssimo obrigado pela explicação muito boa e pela indicação do livro!

Estava bastante ansioso pela sua resposta e, como sempre, me surpreendi!
Mais uma vez, obrigado!

E Vamos lá !