Números complexos UFMG
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Números complexos UFMG
por Fernando_Vieira Dom 22 Jul 2012, 12:46
Por três pontos não colineares do plano complexo,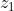 
, 
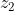e 
, passa uma única circunferência. Sabe-se que um ponto z está sobre essa circunferência se, e somente se, .(z_{1}-z_{3}).(\bar{z_{1}}-\bar{z}).(z_{2}-z))
for um número real. Seja C a única circunferência que passa pelos pontos 
, 
e 
do plano complexo. Assim, DETERMINE todos os pontos do plano complexo cuja parte real é igual a -1 e que estão sobre a circunferência C.
O gabarito é -1 + 4i ou -1 - 4i.
Fernando_Vieira- Padawan
- Mensagens : 56
Data de inscrição : 20/05/2012
Idade : 29
Localização : Belo Horizonte, MG Brasil
Tópicos semelhantes» (UFMG) Os números a,b, e c, nessa ordem
» (UFMG) Se a e b são números reais positivos t
» Números Complexos
» Números complexos
» Números complexos
» (UFMG) Se a e b são números reais positivos t
» Números Complexos
» Números complexos
» Números complexos
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
