Divisibilidade por 9
+3
Al.Henrique
Iago6
Robson Jr.
7 participantes
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
 Divisibilidade por 9
Divisibilidade por 9
Regra de divisibilidade por 9: "Um número é divisível por 9 se a soma de seus algarismos for divisível por 9."
Demonstração:
É fácil ver que as seguintes afirmações são verdadeiras:
i) Todo número da forma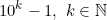 é divisível por 9. Logo
é divisível por 9. Logo 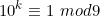 .
.
ii) Todo número é congruente a si mesmo na divisão por qualquer outro.
Suponha, agora, um número da forma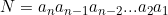 , onde os a's são algarismos das unidades, dezenas etc.
, onde os a's são algarismos das unidades, dezenas etc.
Seguem, de i) e ii), as seguintes relações:

Somando as congruências acima:
 \ mod9\\\\ N \equiv (a_1+a_2+a_3+...+a_n) \ mod9)
CqD
Demonstração:
É fácil ver que as seguintes afirmações são verdadeiras:
i) Todo número da forma
ii) Todo número é congruente a si mesmo na divisão por qualquer outro.
Suponha, agora, um número da forma
Seguem, de i) e ii), as seguintes relações:
Somando as congruências acima:
CqD

Robson Jr.- Fera

- Mensagens : 1263
Data de inscrição : 24/06/2012
Idade : 30
Localização : Rio de Janeiro, RJ

Iago6- Fera

- Mensagens : 808
Data de inscrição : 19/12/2011
Idade : 31
Localização : Natal
 Re: Divisibilidade por 9
Re: Divisibilidade por 9
Eu não consigo entender essas coisas de mod.. :drunken:
Parabéns pela Dem. , Robson!
Parabéns pela Dem. , Robson!
 Re: Divisibilidade por 9
Re: Divisibilidade por 9
Mandou bem!
hygorvv- Elite Jedi

- Mensagens : 1721
Data de inscrição : 15/03/2010
Idade : 35
Localização : Vila Velha
 Re: Divisibilidade por 9
Re: Divisibilidade por 9
Al.Henrique escreveu:Eu não consigo entender essas coisas de mod.. :drunken:
Já deu uma olhada nesse tópico?
https://pir2.forumeiros.com/t10341-teoria-dos-numeros-congruencia-uma-abordagem-objetiva
Tudo está muito bem explicado no pdf lá.

Robson Jr.- Fera

- Mensagens : 1263
Data de inscrição : 24/06/2012
Idade : 30
Localização : Rio de Janeiro, RJ
 Re: Divisibilidade por 9
Re: Divisibilidade por 9
Robson Jr. escreveu:Al.Henrique escreveu:Eu não consigo entender essas coisas de mod.. :drunken:
Já deu uma olhada nesse tópico?
https://pir2.forumeiros.com/t10341-teoria-dos-numeros-congruencia-uma-abordagem-objetiva
Tudo está muito bem explicado no pdf lá.
Boa tarde Robson,
Realmente, não tinha observado esse tópico.
A unica coisa que conheço do "mod" é o básico, seu significado..
Mas não consigo pensar em alguma utilidade. Tavez isso aconteça justamente por não conhecer muito os problemas envolvidos..
Agradeço a indicação
 Re: Divisibilidade por 9
Re: Divisibilidade por 9
Salve Robson!
Ótima demonstração, obrigado por compartilhar conosco
Ótima demonstração, obrigado por compartilhar conosco

Igor Bragaia- Jedi

- Mensagens : 400
Data de inscrição : 24/10/2012
Idade : 27
Localização : Piracicaba, SP, Brasil
 Re: Divisibilidade por 9
Re: Divisibilidade por 9
boa! vou dar uma olhada no tópico sobre mod tb.! =D

Wilson Calvin- Matador

- Mensagens : 524
Data de inscrição : 26/02/2013
Idade : 26
Localização : São Paulo
 Re: Divisibilidade por 9
Re: Divisibilidade por 9
Um número escrito no sistema decimal na forma ab tem valor
10a + b = 9a + (a + b)
Vemos que a primeira parcela é múltipla de nove.
Assim, 10a + b é divisível por 9, se e somente se, 9 | a + b.
Considerando o número escrito no sistema decimal na forma abc. O seu valor é:
100a + 10b + c = 99a + 9b + (a + b + c)
Note que, 99a + 9b = 9(11a + b), um múltiplo de nove.
Logo, 100a + 10b + c é múltiplo de nove, se e somente se, 9 | a + b + c.
Analogamente, concluímos para os demais números.
Assim, "Um número é divisível por 9 se a soma de seus algarismos for divisível por 9."
10a + b = 9a + (a + b)
Vemos que a primeira parcela é múltipla de nove.
Assim, 10a + b é divisível por 9, se e somente se, 9 | a + b.
Considerando o número escrito no sistema decimal na forma abc. O seu valor é:
100a + 10b + c = 99a + 9b + (a + b + c)
Note que, 99a + 9b = 9(11a + b), um múltiplo de nove.
Logo, 100a + 10b + c é múltiplo de nove, se e somente se, 9 | a + b + c.
Analogamente, concluímos para os demais números.
Assim, "Um número é divisível por 9 se a soma de seus algarismos for divisível por 9."

Paulo Ricardo 121- Iniciante
- Mensagens : 16
Data de inscrição : 10/09/2013
Idade : 26
Localização : Boa Vista, Roraima, Brasil
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













