Soma de termos

por Convidado Qua 04 Abr 2012, 20:06

Calcule:
$Soma de termos Gif.latex?\frac{1}{2\cdot3\cdot4}+\frac{1}{3\cdot4\cdot5}+\frac{1}{4\cdot5\cdot6}+..$

Spoiler:

por matheuss_feitosa Qui 05 Abr 2012, 00:18

Observe:

$\frac{1}{2\cdot 3\cdot 4}=\frac12 \cdot (\frac{1}{2\cdot 3}-\frac{1}{3\cdot 4})$

$\frac{1}{3\cdot 4\cdot 5}=\frac12 \cdot (\frac{1}{3\cdot 4}-\frac{1}{4\cdot 5})$

Ou seja, a soma vai se anulando:

$S=\frac{1}{2\cdot 3\cdot 4} + \frac{1}{3\cdot 4\cdot 5} + \frac{1}{4\cdot 5\cdot 6} + ... \frac{1}{2003\cdot 2004\cdot 2005}= \frac12\cdot [(\frac{1}{2\cdot 3}-\frac{1}{3\cdot 4})+(\frac{1}{3\cdot 4} - \frac{1}{4\cdot 5}) + ... +(\frac{1}{2003\cdot 2004}-\frac{1}{2004\cdot 2005})]$

$S=\frac12\cdot [(\frac{1}{2\cdot 3}-\frac{1}{2004\cdot 2005})]=\frac{669669}{2\cdot 2004\cdot 2005}$

Abraços. cheers

por Convidado Qui 05 Abr 2012, 16:14

matheus não entendi aquela primeira passagem, como que você chegou naquela igualdade?

por **JOAO [ITA]** Qui 05 Abr 2012, 17:56

Basta você observar que a sequência:

$2.3.4,\,\,3.4.5,\,\,4.5.6,\,\,...\,\,,2003.2004.2005$

Sempre possuíra a multiplicação de três números consecutivos, e dentre três números consecutivos sempre temos pelo menos um número par, que, tal como um, é divisível por 2, pois se:

$x=a_{0}+a_{1}.10+a_{2}.10^2+...+a_{n}.10^n \\ \\ a_{0}\equiv a_{0}\,\,\,(mod\,\,2)\\ 10\equiv 0\,\,\,(mod\,\,2) =>a_{1}.10\equiv 0\,\,\,(mod\,\,2)\\ ...\\ 10\equiv 0\,\,\,(mod\,\,2)=>10^n\equiv 0\,\,\,(mod\,\,2)=>a_{n}.10^n\equiv 0\,\,\,(mod\,\,2) \\ \\ x=a_{0}+a_{1}.10+a_{2}.10^2+...+a_{n}.10^n\equiv a_{0}\,\,\,(mod\,\,2)$

Logo um número só é divisível por 2 se o seu algarismo das unidades for 0 ou 2.

Daí, sabendo disso, você percebe que todos os termos da sequência :

$\frac{1}{2.3.4}+\frac{1}{3.4.5}+\frac{1}{4.5.6}+...+\frac{1}{2003.2004.2005}$

São fatoráveis por $\frac{1}{2}$ , podendo assim, logo depois de fatorar, verificar a curiosidade de os termos se anularem, reduzindo, dessa forma, os termos dessa Soma Telescópica drasticamente e achando o resultado.

OBS: Essa fatoração por $\frac{1}{2}$ não é nada mais que uma estratégia para se chegar a resolução final.

por Convidado Qui 05 Abr 2012, 20:30

Não João você não entendeu eu disse que não entendi esta parte.(Embora essa demonstração fosse muito da hora):

matheuss_feitosa escreveu:Observe:

$\frac{1}{2\cdot 3\cdot 4}=\frac12 \cdot (\frac{1}{2\cdot 3}-\frac{1}{3\cdot 4})$

Essa parte da diferença. Não da fatoração do meio.

por **JOAO [ITA]** Qui 05 Abr 2012, 22:43

Perdão!

Vou dar uma breve explicação sobre esse tipo de Soma Telescópica:

Naturalmente qualquer seqüência de termos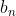 $b_{n}$ pode ser escrita como uma soma telescópica:

$b_{n}=(b_{2}-b_{1})+(b_{3}-b_{2})+...+(b_{n}-b_{n-1})=\\ =\sum_{k=2}^{n}(b_{k}-b_{k-1})$

Esta soma pode ser simplificada da seguinte forma:

$\sum_{k=2}^{n}(b_{k}-b_{k-1})=b_{n}-b_{1}$

.Voltando ao exercício proposto, temos que a sequência pode ser reescrita como:

$\sum_{n=2}^{2003}\frac{1}{n.(n+1).(n+2)}$

.Que pode ser novamente transformada para:

$\sum_{n=2}^{2003}\frac{1}{n.(n+1).(n+2)}=\sum_{n=2}^{2003}\frac{1}{2}.(\frac{1}{n.(n+1)}-\frac{1}{(n+1).(n+2)})=\\ =\frac{1}{2}.[\sum_{n=2}^{2003}(\frac{1}{n.(n+1)}-\frac{1}{(n+1).(n+2)}]$

Que está escrita em uma forma contrária à que eu mostrei no começo:

$\sum_{k=2}^{n}(b_{k-1}-b_{k})=b_{1}-b_{n}$

E aí segue a resolução do matheuss_feitosa.

Obs: Para esse problema você deve ter em mente que:

$\frac{1}{n.(n+1).(n+2).\,\,...\,\,.(n+k)}=\\=\frac{1}{k}.(\frac{1}{n.(n+1).(n+2).\,\,...\,\,.(n+(k-1))}-\frac{1}{(n+1).(n+2).\,\,...\,\,.(n+k)})$

cheers

por matheuss_feitosa Sex 06 Abr 2012, 14:22

Gabriel, a intenção desse tipo de questão é que você simplesmente "perceba" como o produto dos consecutivos deve ser decomposto em diferença. Existem meios de provar, mas não é o mais inteligente a se fazer. Veja:

$\frac{1}{k\cdot (k+1)\cdot (k+2)}\equiv \frac{A}{k\cdot (k+1)}+\frac{B}{(k+1)\cdot (k+2)}$

Resolvendo e achando os valores de A e B:

$\sum_{k=2}^{2003}\frac{1}{k\cdot (k+1)\cdot (k+2)}=\sum_{k=2}^{2003}\frac 12\cdot(\frac{1}{k\cdot (k+1)}-\frac{1}{(k+1)\cdot (k+2)})$

Abraços. :study: :study: cheers

por Convidado Sáb 07 Abr 2012, 11:43

Pode ser insistência minha mas eu não estou conseguindo perceber como transformar esse produto numa diferença. A parte da soma telescópica e tudo mais eu entendi menos aquela transformação.