UFMG/2008
+4
julia.silva
Euclides
Werill
velloso
8 participantes
Página 2 de 2
Página 2 de 2 • 
1, 2
UFMG/2008
por velloso Ter 21 Fev 2012, 00:40
Relembrando a primeira mensagem :
Nesta figura, está representado um quadrado de vértices ABCD:
Sabe-se que as coordenadas cartesianas dos pontos A e B são A = (0, 0) e
B = (3, 4).
Então, é CORRETO afirmar que o resultado da soma das coordenadas do
vértice D é
A) -2.
B) -1.
C) - 1/2
D) - 3/2.
Nesta figura, está representado um quadrado de vértices ABCD:
Sabe-se que as coordenadas cartesianas dos pontos A e B são A = (0, 0) e
B = (3, 4).
Então, é CORRETO afirmar que o resultado da soma das coordenadas do
vértice D é
A) -2.
B) -1.
C) - 1/2
D) - 3/2.
velloso- Estrela Dourada
- Mensagens : 1142
Data de inscrição : 07/04/2010
Idade : 34
Localização : Belém - Pará
Re: UFMG/2008
por velloso Ter 13 Mar 2012, 22:17
A soma de todos os ângulos de um triângulo é 180°.
Se em um triângulo você já tem 90°, então a soma dos outros dois terá que ser 90° (são complementares).
90° + x + y = 180
x + y = 90°
x = 90 - y
Isso é exatamente o que acontece lá, só que com letras trocadas ''a e ''b = 90 - a''.
Entendido, julia?
Se em um triângulo você já tem 90°, então a soma dos outros dois terá que ser 90° (são complementares).
90° + x + y = 180
x + y = 90°
x = 90 - y
Isso é exatamente o que acontece lá, só que com letras trocadas ''a e ''b = 90 - a''.
Entendido, julia?
velloso- Estrela Dourada
- Mensagens : 1142
Data de inscrição : 07/04/2010
Idade : 34
Localização : Belém - Pará
julia.silva- Iniciante
- Mensagens : 13
Data de inscrição : 05/03/2012
Idade : 44
Localização : brasilia
velloso- Estrela Dourada
- Mensagens : 1142
Data de inscrição : 07/04/2010
Idade : 34
Localização : Belém - Pará
Re: UFMG/2008
por Dragondragon Qua 21 Mar 2012, 22:01
Não entendi como se chega nas coordenadas de D através dos catetos, percebi que os triângulos são semelhantes, e que a figura formada é um quadrado.
Alguem consegue fazer por formulas?
Sei que tem outro jeito, tipo se acharmos as coordenas de C o ponto médio de AC é o mesmo de DB aí pelas formulas novamente do ponto médio acharíamos D..
Alguem consegue fazer por formulas?
Sei que tem outro jeito, tipo se acharmos as coordenas de C o ponto médio de AC é o mesmo de DB aí pelas formulas novamente do ponto médio acharíamos D..
Dragondragon- Iniciante
- Mensagens : 2
Data de inscrição : 07/03/2012
Idade : 29
Localização : MG
Re: UFMG/2008
por Jose Carlos Qui 22 Mar 2012, 18:34
- Reta (s) por A e B:
y = (4/3)x
- Reta (t) perpendicular a (s) passando por A:
m = - 3/4
y = ( - 3/4 )x
- Distância AB:
d( A,B ) = 5
- Circunferência de centro C( 0, 0 ) e raio 5:
x² + y² = 25
- Interseção de ( t ) com a circunferência:
25 x² = 400 -> x = - 4 ou x = 4 ( não convém )
x = - 4 -> y = 3
D( - 4, 3 )
S = - 4 + 3 = - 1
y = (4/3)x
- Reta (t) perpendicular a (s) passando por A:
m = - 3/4
y = ( - 3/4 )x
- Distância AB:
d( A,B ) = 5
- Circunferência de centro C( 0, 0 ) e raio 5:
x² + y² = 25
- Interseção de ( t ) com a circunferência:
25 x² = 400 -> x = - 4 ou x = 4 ( não convém )
x = - 4 -> y = 3
D( - 4, 3 )
S = - 4 + 3 = - 1
Jose Carlos- Grande Mestre
- Mensagens : 5551
Data de inscrição : 08/07/2009
Idade : 74
Localização : Niterói - RJ
Re: UFMG/2008
por Leandro Blauth Qua 07 Nov 2012, 08:32
Olá pessoal.
Encontrei essa questão e outra talvez análoga (mas era de calcular a área do quadrado conhecendo as coordenadas de um vértice), numa lista de questões sobre matrizes.
Teria como resolver essa questão usando matrizes?
Encontrei essa questão e outra talvez análoga (mas era de calcular a área do quadrado conhecendo as coordenadas de um vértice), numa lista de questões sobre matrizes.
Teria como resolver essa questão usando matrizes?
Leandro Blauth- Jedi
- Mensagens : 225
Data de inscrição : 13/10/2011
Idade : 31
Localização : Novo Hamburgo, RS, Brasil
Re: UFMG/2008
por victor.ocvb Sex 15 Set 2017, 16:24
Por se tratar de um quadrado, tem-se que:
Distância entre D e A = Distância entre B e A.
Distância entre D e B = Diagonal do quadrado (l√2)
1º Calculando a distância entre A e B.
d(A,B) =
= 5.
2º Calculando a distância entre A e D.
d(A,D)=5=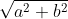
25=
(I)
3º Distância entre B e D
d(D,B) = Diagonal = 5√2.
5√2 =
50 =
Substituindo (I)
4º Encontrar a ordenada (b)
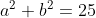
b=3 (Como a ordenada no segundo quadrante é sempre positiva, o valor negativo da equação não interessa).
Como b=3, a=-4. Portanto, -4+3=-1
Distância entre D e A = Distância entre B e A.
Distância entre D e B = Diagonal do quadrado (l√2)
1º Calculando a distância entre A e B.
d(A,B) =
2º Calculando a distância entre A e D.
d(A,D)=5=
25=
3º Distância entre B e D
d(D,B) = Diagonal = 5√2.
5√2 =
50 =
Substituindo (I)
4º Encontrar a ordenada (b)
b=3 (Como a ordenada no segundo quadrante é sempre positiva, o valor negativo da equação não interessa).
Como b=3, a=-4. Portanto, -4+3=-1
victor.ocvb- Iniciante
- Mensagens : 1
Data de inscrição : 12/07/2017
Idade : 25
Localização : Palmas, Tocantins, Brasil
Página 2 de 2 • 1, 2
Tópicos semelhantes» Literatura UFMG 2008
» (UFMG–2008) Um astronauta, de pé sobre a supe
» Mat. funcoes; (UFMG 2008) 3) [Título editado]
» (UFMG)
» (UFMG)
» (UFMG–2008) Um astronauta, de pé sobre a supe
» Mat. funcoes; (UFMG 2008) 3) [Título editado]
» (UFMG)
» (UFMG)
Página 2 de 2
Permissões neste sub-fórum
Não podes responder a tópicos
