Trigonometria no triângulo retangulo

por Fibonacci13 Qua 31 Jan 2024, 19:03

(CESGRANRIO) O valor da área, em [latex]m^{2}[/latex], do triângulo BDA é de, aproximadamente:

Dados:

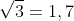
$Trigonometria no triângulo retangulo Png$

Trigonometria no triângulo retangulo 2904712-20230626142906000000-0

A)0,057

B)0,114

C) 0,255

D) 1,14

E) 5,7

Spoiler:

por **Giovana Martins** Qua 31 Jan 2024, 19:32

[latex]\\\mathrm{tan(30^{\circ})=\frac{AD}{BD}\to \frac{\sqrt{3}}{3}=\frac{1,7}{3}=\frac{x}{y+0,3}\ (i)}\\\\ \mathrm{tan(60^{\circ})=\frac{AD}{CD}\to \sqrt{3}=1,7=\frac{x}{y}\ (ii)\ \therefore\ (x,y)=\left ( \frac{51}{200},\frac{3}{20} \right )}\\\\ \mathrm{[BDA]=\frac{BD\cdot AD}{2}=\frac{1}{2}\cdot \left ( \frac{3}{20}+0,3 \right )\cdot \frac{51}{200}\approx 0,057\ m^2}[/latex]

Trigonometria no triângulo retangulo

Trigonometria no triângulo retangulo

Re: Trigonometria no triângulo retangulo

Um fórum livre e democrático.