Pontos Notáveis do Triângulo

Seja ABC um triângulo com circuncentro O. Denote por [latex]H_A, H_B, H_c[/latex] os simétricos do ortocentro H em relação aos lados BC, CA, AB, respectivamente. Analise as afirmações:

I. [latex]([AH_CBH_ACH_B]=2[ABC])[/latex]

II. Se N é o ponto médio do lado AC e D é o pé da altura por A, então [latex]DN \bot BH_A[/latex]

III. [latex]([BH_ACO]=\frac{[ABH_AC]}{2})[/latex]

IV. [latex]H_AD= \frac{BD \cdot DC}{AB}[/latex]

Quantas são verdadeiras?

Resposta :

Alguém pode me ajudar com as 3 primeiras? Eu acredito que a 1 e a 3 estão se referindo às áreas dessas figuras, mas não consigo achar uma relação entre elas. A segunda eu nem tenho ideia de por onde começar.

Demonstração da III alternativa:

 [latex]\overline{CD}[/latex]=x ; [latex]\overline{BD}[/latex] = y ; [latex]\overline{H_AD}[/latex] = h ; [latex]\overline{AD}[/latex] = h' ; altura do triângulo COB=H'

[[latex]ABH_AC[/latex]]= [latex]\frac{(h+h')(x+y)}{2}[/latex]
[[latex]BH_ACO[/latex]]= [latex]\frac{(x+y)(h+H')}{2}[/latex]

Só que, o triângulo [latex]AOH_A[/latex] é isósceles, portanto a sua altura divide [latex]\overline{AH_A}[/latex] em duas medidas de mesmo valor, igual a (h+h')/2. Por meio da geometria do problema, fica evidente que essa medida é igual a (h+H'). Logo, substituindo essa informação na área do quadrilátero, fica:

[[latex]BH_ACO[/latex]]=[latex]\frac{(x+y)(h+h')}{4}[/latex]=[[latex]ABH_AC[/latex]]/2


Demonstração da alternativa I:

Da imagem acima, a área do triângulo [latex]BH_AC[/latex] é idêntica à área do BHC, isso acontece pq, como [latex]H_A[/latex] é o simétrico de H, a distância deles ao segmento BC são as mesmas e, já que possuem a mesma base, o produto b.h/2 é o mesmo para esses dois triângulos. Isso vai acontecer para os outros dois triângulos que são externos a ABC, internos à circunferência e que compõem o polígono analisado. Logo, a área do polígono é [latex](ABC) + (BH_AC) + (CH_BA) + (AH_CB) = 2(ABC)[/latex]


Ainda não consegui mostrar a II, se alguém tiver alguma ideia, manda aq pfv.

Bom dia.


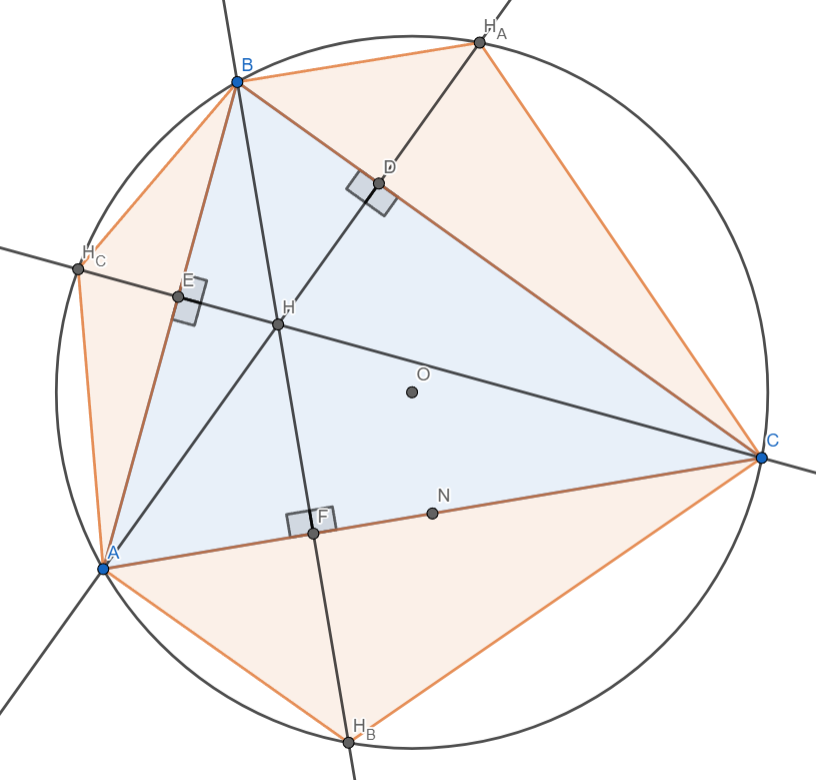
Para a primeira alternativa basta mostrar que:

[latex] ([AH_B C]) = ([AHC]) [/latex]  [latex]([AH_C B]) = ([AHB])[/latex] e [latex]([BH_A C]) = ([BHC])[/latex]


Vou demonstrar que [latex] ([AH_B C]) = ([AHC]) [/latex], o restante é análogo.


Seja [latex]\angle ACH_B = \alpha \Rightarrow \angle CH_B B = 90 - \alpha \Rightarrow \angle BAC = 90 - \alpha \Rightarrow \angle ACH = \alpha \Rightarrow \triangle HCF \equiv \triangle H_B CF [/latex]
 (caso ALA)


 analogamente temos que:
[latex]\triangle HAF \equiv \triangle H_B AF \Rightarrow \triangle AH_B C \equiv \triangle AHC \Rightarrow ([AH_B C]) = ([AHC])[/latex]






Para a segunda alternativa, observe:

DN é mediana relativa à hipotenusa, portanto DN = AN = NC, agora basta completar os ângulos, fica de exercício.