Geometria Plana
3 participantes
Página 1 de 1
Geometria Plana
por Eduardo12345 Sáb 06 Ago 2022, 13:48
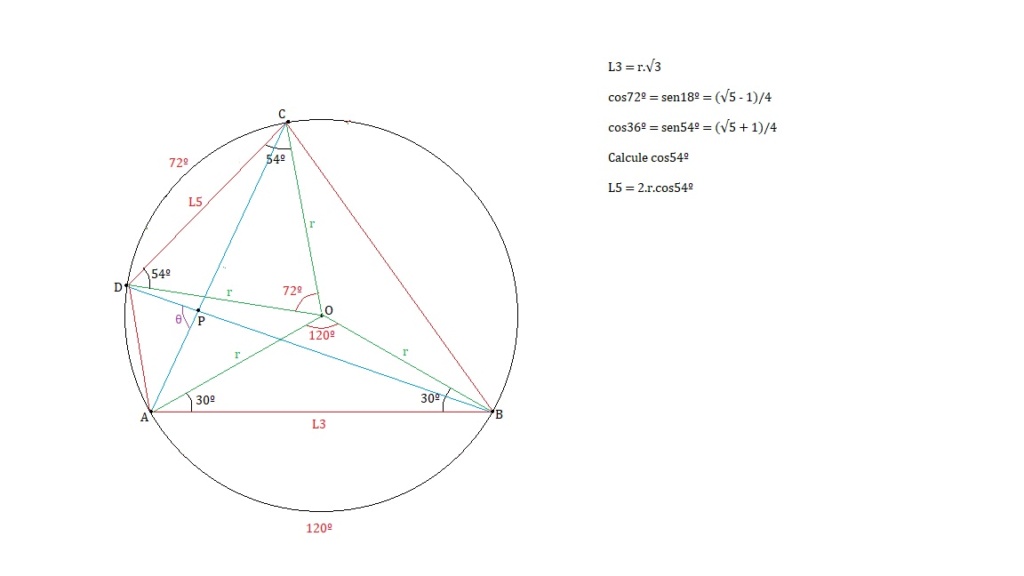
Calcule a medida do menor ângulo que determina as diagonais de um quadrilátero ABCD, inscrito em uma circunferência, se os lados AB e CD são equivalentes aos lados do triângulo equilátero e pentágono regular, inscritos na dita circunferência.
A)9°
B)18°
C)6°
D)66°
E)12°
R:C
A)9°
B)18°
C)6°
D)66°
E)12°
R:C
Eduardo12345- Iniciante
- Mensagens : 47
Data de inscrição : 19/02/2022
Elcioschin- Grande Mestre
- Mensagens : 73163
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Geometria Plana
por petras Dom 07 Ago 2022, 09:35
Estou encontrando um valor bem diferente das alternativas. Aproveitando o desenho do Élcio
[latex]\angle CDO = \frac{\angle CDA}{2} =\frac{108}{2} = 54^o\\ \angle BAO = \frac{\angle BAC}{2} =\frac{60}{2} = 30^o\implies \angle AOB =120^o\\ \angle DPA = 180^o - \angle ADP - \angle PAD\\ \angle ADP = \frac{\angle AOB}{2}=\frac{120}{2} = 60^o\\ \angle PAD = \frac{\angle DOC}{2}=\frac{72}{2} = 36^o\\ \therefore \boxed{\angle \theta = 180-60-36=84^o}\color{green}\checkmark [/latex]
Mesmo se fosse o ângulo da diagonal com a lateral(< DCA) teríamos 24o
Alguém poderia comentar?
[latex]\angle CDO = \frac{\angle CDA}{2} =\frac{108}{2} = 54^o\\ \angle BAO = \frac{\angle BAC}{2} =\frac{60}{2} = 30^o\implies \angle AOB =120^o\\ \angle DPA = 180^o - \angle ADP - \angle PAD\\ \angle ADP = \frac{\angle AOB}{2}=\frac{120}{2} = 60^o\\ \angle PAD = \frac{\angle DOC}{2}=\frac{72}{2} = 36^o\\ \therefore \boxed{\angle \theta = 180-60-36=84^o}\color{green}\checkmark [/latex]
Mesmo se fosse o ângulo da diagonal com a lateral(< DCA) teríamos 24o
Alguém poderia comentar?
Última edição por petras em Dom 07 Ago 2022, 10:37, editado 1 vez(es)
____________________________________________
_______________________________
"Ex nihilo nihil fit"
petras- Monitor
- Mensagens : 2117
Data de inscrição : 10/06/2016
Idade : 59
Localização : bragança, sp, brasil
Re: Geometria Plana
por Elcioschin Dom 07 Ago 2022, 10:29
Concordo com o Petras.
Apenas esclarecendo
A^DP = ADB é ângulo inscrito que subtende arco de 120º --->
A^DP = A^DB = 120º/2 = 60º
DÂP = DÂC é ângulo inscrito que subtende arco de 72º --->
DÂC = DÂP = 72º/2 = 36º
Apenas esclarecendo
A^DP = ADB é ângulo inscrito que subtende arco de 120º --->
A^DP = A^DB = 120º/2 = 60º
DÂP = DÂC é ângulo inscrito que subtende arco de 72º --->
DÂC = DÂP = 72º/2 = 36º
Elcioschin- Grande Mestre
- Mensagens : 73163
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tópicos semelhantes» Geometria analítica com geometria plana
» FME 9-Geometria Plana
» Geometria Plana
» Geometria plana
» Geometria Plana
» FME 9-Geometria Plana
» Geometria Plana
» Geometria plana
» Geometria Plana
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
