Otimização em uma fábrica de caixas de papelão

por leuname027askgkjg/~l/ll Sáb 11 Jun 2022, 10:48

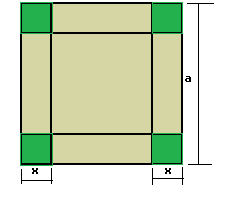
Na figura, em anexo, vemos um papelão quadrado com 12100 cm² de área, que deve ser transformado em uma caixa sem tampa. Determine a medida x do lado de cada quadrado que será retirado nos quatro cantos do papelão, a fim de se maximizar volume.

Otimização em uma fábrica de caixas de papelão Maximi12

[latex]A=L^{2}\rightarrow 12100=L^{2}\rightarrow L=110[/latex]

OBS: Gostaria de uma resolução sem derivada, ao tentar fazê-la fiquei travado em:
[latex]A=((110-2x)^{2})x \rightarrow A=(4x^{2} -440x +12100)x\rightarrow A=(4(x^{2} -110x + 3025))x\rightarrow A=4x(x-55)^{2}\rightarrow 12100=4x(x-55)^{2}\rightarrow \frac{12100}{(x-55)^{2}}=4x\rightarrow x=\frac{\frac{12100}{(x-55)^{2}}}{4}\rightarrow x=\frac{12100\cdot 1}{^{(x-55)^{2})\cdot 4}}\rightarrow [/latex]

por **qedpetrich** Sáb 11 Jun 2022, 11:13

Olá Leu;

Desenvolvendo:

$Otimização em uma fábrica de caixas de papelão Png$

$Otimização em uma fábrica de caixas de papelão Png.latex?%5Cdpi%7B100%7D%20%5Cmathrm%7BV%28x%29%3D%28a-2x%29%5E2.x%20%3D%20%28110-2x%29%5E2.x%3D%284x%5E2-440x+12100%29$

Note que temos a multiplicação de uma reta (x) com a parábola (4x² - 440x + 12100). Para que o volume seja máximo, basta tomar o x_vda função quadrática, dessa forma:

V_máx → Quando x = x_v

Logo:

$Otimização em uma fábrica de caixas de papelão Png.latex?%5Cdpi%7B100%7D%20%5Cmathrm%7Bx_%7Bv%7D%3D%5Cfrac%7B440%7D%7B2$

Otimização em uma fábrica de caixas de papelão

Otimização em uma fábrica de caixas de papelão

Re: Otimização em uma fábrica de caixas de papelão

Um fórum livre e democrático.