(UnB) Caixas de Papelão

Uma empresa fabricante de caixas de papelão tem uma encomenda para fabricar caixas de base quadrada, sem tampa, com capacidade para 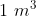. Se metros é o comprimento de um dos lados da base da caixa, e considerando , em 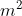, a área total da superfície lateral da caixa, julgue os itens abaixo.

(1) O domínio da função é o conjunto dos números reais.
(2) A caixa de menor superfície lateral que a empresa pode fabricar com a
capacidade desejada tem dimensão igual a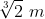 , em cada lado da base.
(3) Se a caixa encomendada tivesse tampa, a caixa com menor superfície
lateral, com capacidade para armazenar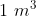 , seria fabricada com 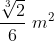de papelão.

Spoiler:

Aldrin

Suponho que "área lateral" seja a área total do papelão, incluindo a base;

Seja h a altura da caixa ----> V = x²*h ----> 1 = x²*h ----> h = 1/x²


A(x) = x² + 4*x*h ----> A*x² = x² + 4*x*(1/x²) ----> A(x) = x² + 4/x -----> Derivando e igualando a zero:

A'(x) = 2x - 4/x² ----> 2x - 4/x² = 0 -----> 2x = 4/x² ----> x³ = 2 ----> x = ³\/2

a) O domínio é o conjunto dos reais POSITIVOS ----- Errada

b) x = ³\/2 -----> Certa

c) A(x) = 2x² + 4/x ----> A'(x) = 4x - 4/x² = 0 ----> x = 1 ----> A(x) = 6 m² ----> Errada