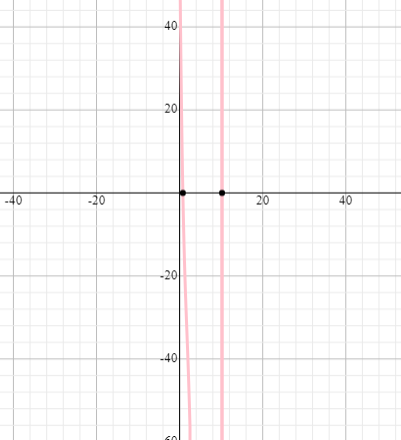
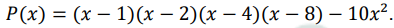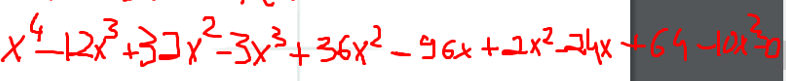Polinômio de quarto grau (ou segundo?)
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Polinômio de quarto grau (ou segundo?)
Polinômio de quarto grau (ou segundo?)
Última edição por MarlonBrSKOITO em Sex 22 Abr 2022, 23:41, editado 1 vez(es)

MarlonBrSKOITO- Jedi

- Mensagens : 235
Data de inscrição : 01/06/2019
Idade : 22
Localização : Barbacena MG
 Re: Polinômio de quarto grau (ou segundo?)
Re: Polinômio de quarto grau (ou segundo?)
Olá Marlon;
Não é porque o polinômio apresenta somente duas raízes como solução, que o polinômio será do segundo grau. Se x está elevado na 4 potência, então esse é caracterizado como quarto grau.
Veja a semelhança entre duas funções.
f(x) = x^2
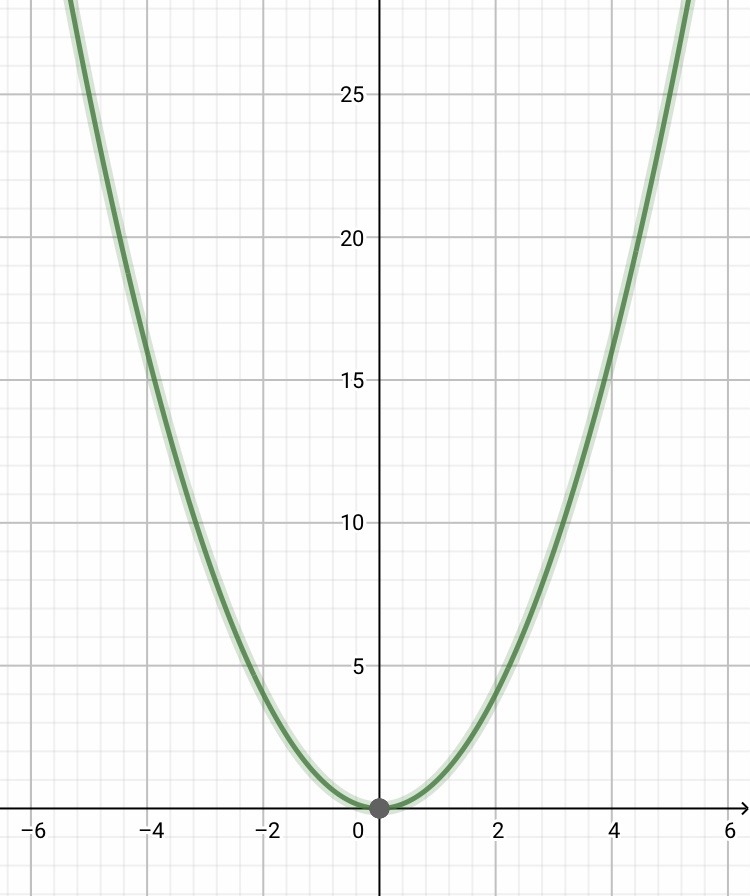
g(x) = x^4
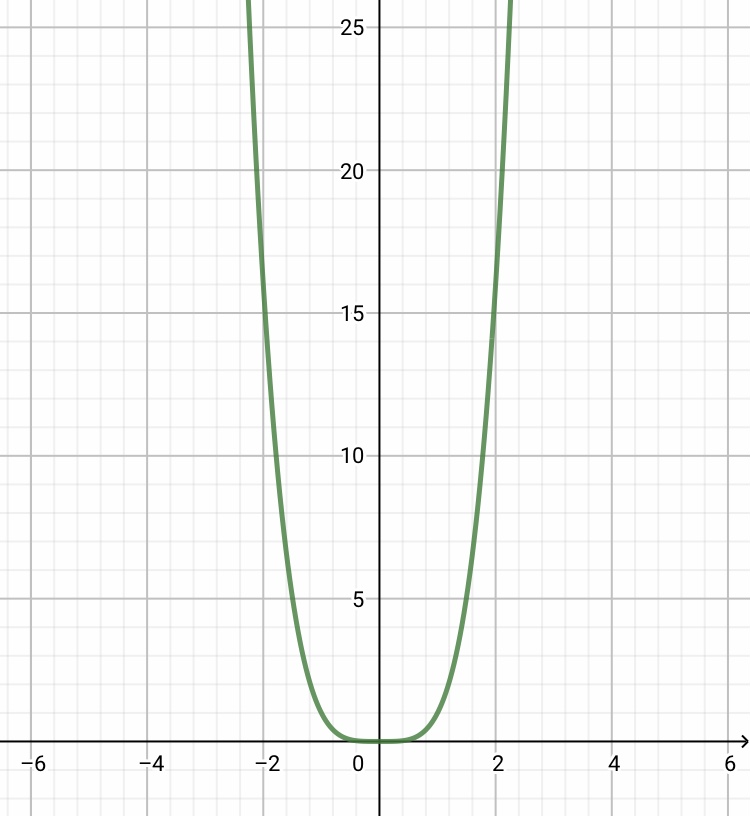
As duas funções são muito semelhantes, mas não são iguais.
Não é porque o polinômio apresenta somente duas raízes como solução, que o polinômio será do segundo grau. Se x está elevado na 4 potência, então esse é caracterizado como quarto grau.
Veja a semelhança entre duas funções.
f(x) = x^2

g(x) = x^4

As duas funções são muito semelhantes, mas não são iguais.
____________________________________________
Dê tempo ao
Lateralus Φ

qedpetrich- Monitor

- Mensagens : 2498
Data de inscrição : 05/07/2021
Idade : 24
Localização : Erechim - RS / Passo Fundo - RS
Rory Gilmore gosta desta mensagem
 Re: Polinômio de quarto grau (ou segundo?)
Re: Polinômio de quarto grau (ou segundo?)
Mas se ele é do quarto grau, não tem que ter 4 raízes? Não entendi

MarlonBrSKOITO- Jedi

- Mensagens : 235
Data de inscrição : 01/06/2019
Idade : 22
Localização : Barbacena MG
 Re: Polinômio de quarto grau (ou segundo?)
Re: Polinômio de quarto grau (ou segundo?)
g(x) = x⁴ também é do quarto grau e só tem uma raiz. E agora? *SUSPENSE* 
Se fosse esse caso, então em polinômios de segundo grau com raízes duplas deveriam ser considerados polinômios do primeiro grau, o quê não faz sentido algum. Ser do primeiro grau, do segundo grau ou do terceiro grau está relacionado a potência que x está elevado, não necessariamente, a quantidade de raízes do polinômio. O que se pode afirmar, é que o máximo de raízes que um polinômio de quarto grau pode admitir são quatro raízes.

Se fosse esse caso, então em polinômios de segundo grau com raízes duplas deveriam ser considerados polinômios do primeiro grau, o quê não faz sentido algum. Ser do primeiro grau, do segundo grau ou do terceiro grau está relacionado a potência que x está elevado, não necessariamente, a quantidade de raízes do polinômio. O que se pode afirmar, é que o máximo de raízes que um polinômio de quarto grau pode admitir são quatro raízes.
____________________________________________
Dê tempo ao
Lateralus Φ

qedpetrich- Monitor

- Mensagens : 2498
Data de inscrição : 05/07/2021
Idade : 24
Localização : Erechim - RS / Passo Fundo - RS
Medeiros e Rory Gilmore gostam desta mensagem
 Re: Polinômio de quarto grau (ou segundo?)
Re: Polinômio de quarto grau (ou segundo?)
Ô Marlon, então, seguindo seu raciocínio, um polinômio sem raízes reais (apenas imaginárias, ex: y = x² + 5) seria do grau zero? E f(x)= 0 é um polinômio do grau infinito pois, sendo o próprio eixo dos x, teria infinitas raízes?

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
qedpetrich gosta desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» Polinômio de quarto grau
» polinômio do quarto grau
» Questão UFRN Equação do Segundo e Quarto Grau
» Como fatorar esse polinômio do quarto grau?
» polinômio do segundo grau
» polinômio do quarto grau
» Questão UFRN Equação do Segundo e Quarto Grau
» Como fatorar esse polinômio do quarto grau?
» polinômio do segundo grau
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos