Matemática - Números Complexos (DESAFIO II)

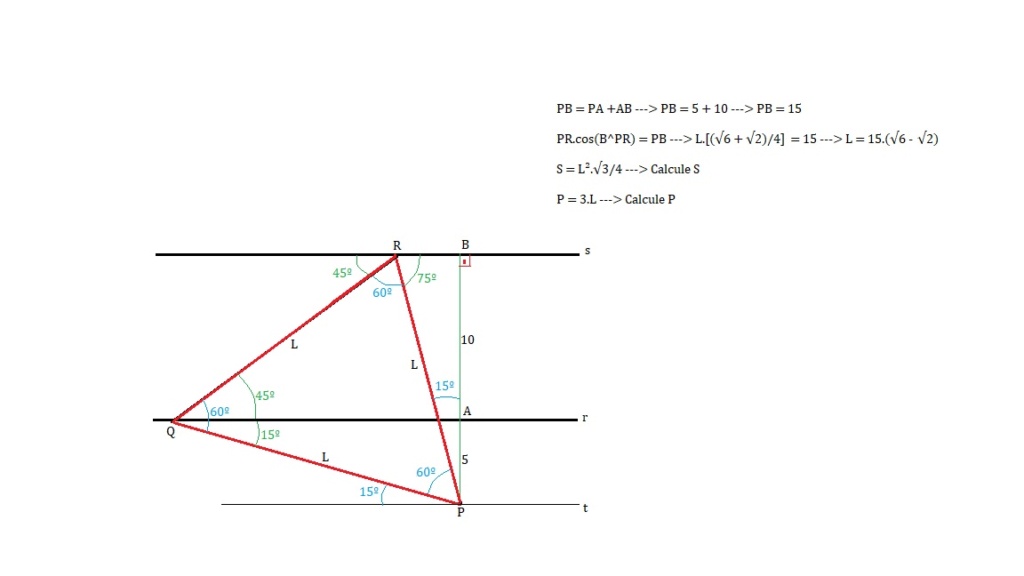
2) Sejam r e s duas retas paralelas distando 10 cm entre si. Seja P um ponto no plano definido por r e s e exterior à região limitada por estas retas, distando 5 cm de r. As respectivas medidas da área e do perímetro, em cm² e em cm, do triângulo equilátero PQR cujos vértices Q e R estão, respectivamente, sobre as retas r e s, são iguais a:

a) [latex]175\frac{\sqrt{3}}{3}[/latex] e [latex]5\sqrt{21}[/latex]

b) [latex]175\frac{\sqrt{3}}{3}[/latex] e [latex]10\sqrt{21}[/latex]

c) [latex]175\sqrt{3}[/latex] e [latex]10\sqrt{21}[/latex]

d) [latex]175\sqrt{3}[/latex] e [latex]5\sqrt{21}[/latex]

e) [latex]700[/latex] e [latex]10\sqrt{21}[/latex]

Não tenho o gabarito. 

Desde já, muitíssimo obrigado pela ajuda!!

Mas como sabias que o triângulo teria esses ângulos? E por que o o ponto P não pode estar no meio das retas? Só gostaria de saber como montar a imagem

O enunciado diz que o triângulo é equilátero, logo os ângulos do triângulo valem 60º

O enunciado diz que o ponto P é exterior às duas retas e dista 5 cm da reta r, logo ele só pode estar abaixo de r (na minha figura).

Para demonstrar os demais ângulos, faça B^PR = θ e calcule todos os demais em função de θ. Depois, prove que θ = 15º

um modo malandro de responder (e vergonhoso num fórum).

Suponha que alguma das alternativas é verdadeira.
Mentalmente já podemos ver que o lado do triângulo deve ser maior que 10+5 , ou seja, L > 15. Se houver dificuldade com isto, veja o desenho do Élcio.
E, por ser mais fácil, vamos considerar o perímetro das alternativas. Se o perímetro é 5√21, podemos aproximar por 5*4,5 = 22,5 , logo o lado seria 22,5/3 = 7,5. Evidente que não é isto pois é muito menor que 15, logo o perímetro deve ser uma das outras três alternativas, 10√21, e portanto o lado será:
L = 10√21/3.

A área é S = L².√3/4 = (100.21/9).√3/4 = (25.7/3).√3 = 175.√3/3

alternativa (b)

Por se tratar de uma questão de múltipla escolha, esta "malandragem" economiza um grande tempo!