matemática - função

por Júliawww_520 Dom 10 Abr 2022, 10:29

Seja f uma função real definida para todo x real tal que: ƒ é ímpar; ƒ(x + y) = ƒ(x) + ƒ(y); e ƒ(x) ≥ 0, se x ≥ 0. Definindo g(x)= f(x) - f(1) / x , se x ≠ 0. Sendo n um número natural, podemos afirmar que:

a) f é não decrescente e g é uma função ímpar.
b) f é não decrescente e g é uma função par.
c) f é não decrescente e 0 ≤ g(n) ≤ f(1).
d) f não é monótona e 0 ≤ g(n) ≤ f(1).
e) não é possível garantir que 0 ≤ g(n) ≤ f(1).

Como ele garante essa proposição?

por Fibonacci13 Dom 10 Abr 2022, 15:06

Olá, Júlia. Olha a resolução que achei.

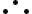
A função é ímpar, então $matemática - função Mimetex_$

$matemática - função Mimetex_$ $matemática - função Mimetex_$ $matemática - função Mimetex_$

$matemática - função Mimetex_$

$matemática - função Mimetex_$

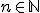Por indução, vemos que $matemática - função Mimetex_$ :

$matemática - função Mimetex_$

Como, $matemática - função Mimetex_$ e $matemática - função Mimetex_$ , temos que :

$matemática - função Mimetex_$

Portanto, como $matemática - função Mimetex_$ , conclui-se que $matemática - função Mimetex_$

Admitindo $matemática - função Mimetex_$ e como $matemática - função Mimetex_$ e $matemática - função Mimetex_$ , temos :

$matemática - função Mimetex_$ , portanto ela é não-decrescente.

Creio que seja o necessário para afirmar que a letra C está correta

por Júliawww_520 Seg 11 Abr 2022, 10:09

Fibonacci13 escreveu:
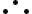
A função é ímpar, então $matemática - função Mimetex_$

$matemática - função Mimetex_$ $matemática - função Mimetex_$ $matemática - função Mimetex_$

$matemática - função Mimetex_$

Por indução, vemos que $matemática - função Mimetex_$

Olá! Eu não entendi essa parte da resolução. Poderia me explicar de onde surgiu esse $matemática - função Mimetex_$ ?

por Fibonacci13 Seg 11 Abr 2022, 10:31

Júlia, acredito que seja a seguinte ideia.

Ele adota x = 1 e y = -1.

f(x-y) = f(x) - f(y)

f(1+1) = f(1) - f(-1)

Se f(x) = -f(-x)

Então: -f(-1) = f(1)

Logo:

f(1+1) = f(1) -f(-1) ----> f(1+1) = f(1) + f(1) = f(1+1) = 2f(1) = f(2).

por Júliawww_520 Seg 11 Abr 2022, 10:43

Fibonacci13 escreveu:Ele adota x = 1 e y = -1.

f(x-y) = f(x) - f(y)

f(1+1) = f(1) - f(-1)

Se f(x) = -f(-x)

Como ele adota Y = -1?

por Fibonacci13 Seg 11 Abr 2022, 10:53

Bom, acredito que ai foi escolha dele. Normalmente em exercícios desse tipo, eu vejo o povo adotando valores entre -2,-1,0,1,2. Eles vão jogando valores até chegar em alguma conclusão.

por Júliawww_520 Seg 11 Abr 2022, 11:03

Fibonacci13 escreveu:Bom, acredito que ai foi escolha dele. Normalmente em exercícios desse tipo, eu vejo o povo adotando valores entre -2,-1,0,1,2. Eles vão jogando valores até chegar em alguma conclusão.

Ah, entendi. Então era um valor representativo...