ENEM 2018 - Teoria dos conjuntos

por Bruna Lourenci Qua 23 Fev 2022, 12:11

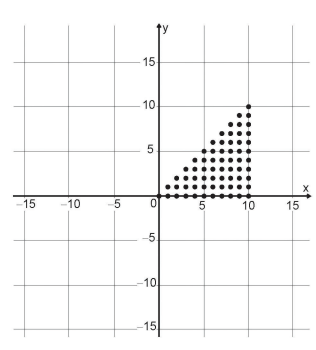
Para criar um logotipo, um profissional da área de design gráfico deseja construí-lo utilizando o conjunto de pontos do plano na forma de um triângulo, exatamente como mostra a imagem.

ENEM 2018 - Teoria dos conjuntos Sem_tz10

Para construir tal imagem utilizando uma ferramenta gráfica, será necessário escrever algebricamente o conjunto que representa os pontos desse gráfico.

Esse conjunto é dao pelos pares ordenados (x;y) e [latex]\mathbb{N}x\mathbb{N}[/latex], tais que:

a) [latex]0\leq x\leq y\leq 10[/latex]

b) [latex]0\leq y\leq x\leq 10[/latex]

c) [latex]0\leq x\leq 10\leq y\leq 10[/latex]

d) [latex]0\leq x + y\leq 10[/latex]

e) [latex]0\leq x + y\leq 20[/latex]

Gabarito: B) [latex]0\leq y\leq x\leq 10[/latex]

Alguém pode me ajudar, por favor? Não consigo entender por que a letra c está errada. Também não consegui compreender a diferença entre a letra a e a letra b. pale

por **Rory Gilmore** Qua 23 Fev 2022, 12:46

Primeiro observe que [latex]0\leq x\leq 10[/latex].

A reta passando por (0, 0) e (10, 10) é da forma:
y = ax
10 = a.10
a = 1

Portanto a reta é y - x = 0. Tomamos o ponto (5, 0) abaixo da reta para verificar seu sinal, isso resulta em - 5 < 0. Logo, temos que tomar os pontos com [latex]y - x \leq 0[/latex].

Então os pontos (x, y) devem satisfazer:
i)[latex]0\leq x\leq 10[/latex]
e
ii)[latex]y - x \leq 0[/latex]
[latex]y \leq x[/latex]

Juntando as duas desigualdades vem:
[latex]0\leq y\leq x\leq 10[/latex].

Um pouco mais: dada uma reta, por exemplo y - x = 0, verificamos se o semiplano abaixo ou acima da reta é positivo ou negativo simplesmente substituindo um ponto do semiplano na equação da reta e verificando o seu sinal. No caso desse exercício, tomamos o ponto abaixo da reta (5, 0) para verificar qual é o sinal da região abaixo da reta e obtemos que é uma região de sinal negativo ou seja y - x < 0 em todo semiplano abaixo da reta.

por Bruna Lourenci Qua 23 Fev 2022, 13:04

Rory Gilmore escreveu:Primeiro observe que [latex]0\leq x\leq 10[/latex].

A reta passando por (0, 0) e (10, 10) é da forma:
y = ax
10 = a.10
a = 1

Portanto a reta é y - x = 0. Tomamos o ponto (5, 0) abaixo da reta para verificar seu sinal, isso resulta em - 5 < 0. Logo, temos que tomar os pontos com [latex]y - x \leq 0[/latex].

Então os pontos (x, y) devem satisfazer:
i)[latex]0\leq x\leq 10[/latex]
e
ii)[latex]y - x \leq 0[/latex]
[latex]y \leq x[/latex]

Juntando as duas desigualdades vem:
[latex]0\leq y\leq x\leq 10[/latex].

Um pouco mais: dada uma reta, por exemplo y - x = 0, verificamos se o semiplano abaixo ou acima da reta é positivo ou negativo simplesmente substituindo um ponto do semiplano na equação da reta e verificando o seu sinal. No caso desse exercício, tomamos o ponto abaixo da reta (5, 0) para verificar qual é o sinal da região abaixo da reta e obtemos que é uma região de sinal negativo ou seja y - x < 0 em todo semiplano abaixo da reta.

Certo, mas por que a reta é y - x = 0? E como vou chegar nessa conclusão sabendo o valor de a?

por **Rory Gilmore** Qua 23 Fev 2022, 13:15

Uma reta passando pela origem (0, 0) tem sempre a equação dada por:
y = ax e encontramos que a = 1 porque a reta também passa pelo ponto (10, 10). Substituindo a = 1 na reta y = ax decorre:
y = 1.x
y - x = 0

Então, a reta que limita toda a parte do plano cartesiano onde estão os pontos de interesse tem equação y - x = 0.

por Bruna Lourenci Qua 23 Fev 2022, 15:22

Rory Gilmore escreveu:Uma reta passando pela origem (0, 0) tem sempre a equação dada por:
y = ax e encontramos que a = 1 porque a reta também passa pelo ponto (10, 10). Substituindo a = 1 na reta y = ax decorre:
y = 1.x
y - x = 0

Então, a reta que limita toda a parte do plano cartesiano onde estão os pontos de interesse tem equação y - x = 0.

Agora entendi! Muito obrigada! ENEM 2018 - Teoria dos conjuntos 503132