IME 2016 - Cone inscrito

IME(2015/2016) - Um cone é inscrito em um quadrilátero ABCDEFGH de forma que a base do cone é o círculo inscrito na base ABCD. O vértice do cone é o centro da face oposta do cubo. A projeção do vértice H na base ABCD coincide com o vértice D. Determine a área da seção do cone pelo plano ABH em função de a, a medida da aresta do cubo.

Gabarito: (πa²√6)/18

Pessoal, encontrei essa resolução aqui (tinha no FB e no Ari de Sá também, mas essa do Bernoulli parecia melhor) http://www.bernoulliresolve.com.br/provas/2015/ime/2dia/index.html# (é a questão 10) e não consegui entender o porquê cos 45º / cos α = e. Fiz até um esboço pra tentar entender, mas não consegui enxergar como definiram a excentricidade da elipse com ângulos em um plano diferente do plano da elipse. Alguém poderia me elucidar?

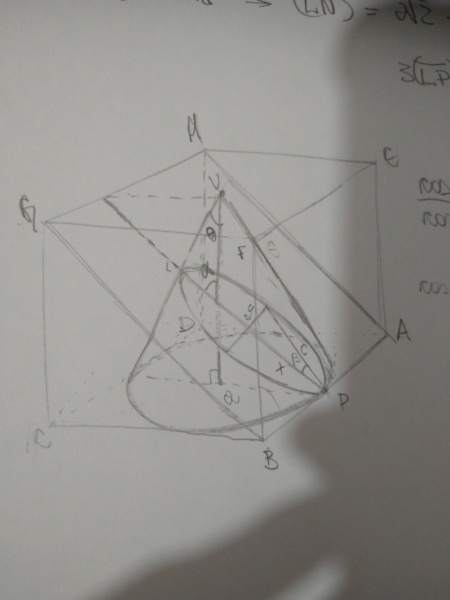
Meu esboço: 

Gio, felizmente, já conheço o Teorema. Obrigado por me lembrar. Estou tentando aplicá-lo pra ver se chego em algo. Por enquanto, sem sucesso. Encontrei outro modo de resolver o exercício, mas ainda estou curioso com essa relação encontrada. Vou continuar tentando, mas sinto que me estão esgotando as ideias. Se puder me dar uma forcinha, ficaria muito grato. 

Finalmente consegui! Vou deixar as duas resoluções que propus ao exercício, com as devidas demonstrações necessárias ao completo entendimento.

Antes de partir às resoluções, é importante que tenhamos o desenho da figura em questão. Fiz um esboço da ideia, vejam:



Notem, primeiramente, que o plano ABH contém também o vértice G, de modo que podemos denominá-lo plano ABGH. A interseção do plano com o cone, nesse caso, resulta em uma elipse. Isso vem das próprias definições de cônicas (figuras formadas a partir de planos traçados em cones). Assim, o exercício nos pede que determinemos a área da elipse hachurada. 

A partir do estudo das cônicas, sabe-se que a área da elipse é dada por π.x.y, onde x é o semieixo maior e y o semieixo menor. Precisamos, então, descobrir os semieixos da elipse para, finalmente, concluir o valor da área.

Ótimo, agora que já sabemos o que fazer, partamos a análise da figura. Podemos tomar, em um primeiro momento, a projeção formada pela figura no plano PJKW, paralelo a BCGF e passando por V, ter-se-á a seguinte figura:



Analisando-se a figura, nota-se que ∆LVK e ∆JLP são semelhantes pelo caso AA. Nesse sentido, podemos escrever que [JP]/[KV] = [KL]/[LP]. Como [JP] = a e [KV] = a/2, vem: [KL]/[LP] = 1/2 ⇒ [LP] = 2[KL] (i). Verifica-se, agora, que [KP] é a diagonal de um quadrado e, portanto, [KP] = [LP] + [KL] = a√2 (ii). De (i) e (ii), tem-se: [LP] = (2a√2)/3. Como [LP] corresponde ao eixo maior da elipse, então o seu semieixo maior, x, vale [LP]/2, daí: x = (a√2)/3.

Em posse de x, busquemos, agora, y. É nesse momento que as duas resoluções se diferenciam. Partamos, então, a cada uma delas. 



Primeira resolução:

Nesse caso, iremos encontrar o valor de y a partir de uma esfera auxiliar. Traçando-se uma esfera auxiliar que contenha os pontos determinantes do eixo menor, tem-se:

 

Notem que a esfera circunda o eixo menor passando pelos pontos extremos desse. Representando a projeção dessa esfera, teremos:



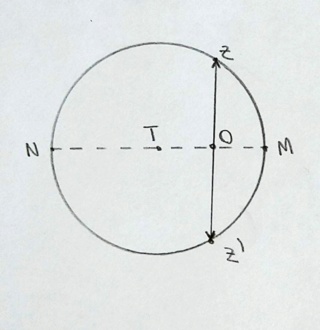
Percebam que, denominei os pontos N e M de forma que [NM] seja perpendicular ao eixo menor, o qual denominei [ZZ']. Podemos, aqui, aplicar a potência de ponto em O, de forma que: [ZO][Z'O] = [MO][NO]. Como [ZO] = [Z'O] = y, tem-se: y² = [MO][NO]. Precisamos, portanto, desses valores. Para isso, voltemos a projeção em PJKW, colocando, agora, os novos pontos da esfera. Vejam:



Aqui, notem que ∆PRT' e ∆OTT' são semelhantes. Assim: [PR]/[OT] = [PT']/[OT']. Como [OT'] = [PT'] - [PO], vem: [PR]/[OT] = [PT']/([PT'] - [PO]). Sendo [PO] o semieixo maior, tem-se [PO] = (a√2)/3. Como [PR] = a/2 e [PT'] = (a√2)/2, na equação, ter-se-á: [OT] = a/6. Como ∆PMO e ∆PVK são semelhantes, vem: [MO]/[VK] = [PO]/[PK]. Sendo [PO] = (a√2)/3, [PK] = a√2 e [VK] = a/2, tem-se: [MO] = a/6.

Voltemos, agora, a esfera. Como [NO] = [NM] - [OM] e [NM] = 2([OT] + [OM]), vem: [NO] = 2([OT] + [OM]) - [OM] = 2[OT] + [OM]. Pela equação da potência de ponto: y² = [MO][NO] ⇒ y² = (a/6)[(2a/6) + (a/6)] ⇒ y² = 3a²/36 ⇒ y = (a√3)/6.

Finalmente, na equação da área: A_elipse = π.x.y = π.[(a√2)/3](a√3)/6 ⇒ A_elipse = (πa²√6)/18.



Segunda resolução:

Nesse caso, iremos utilizar a ideia de excentricidade da elipse para definir o eixo menor e, daí, calcular a área. É uma solução um pouco complexa, mas extremamente rica em conhecimento. Lembrando, inicialmente, que a excentricidade da elipse é uma relação entre o seu semieixo maior e sua distância focal. Assim, pode-se definir e = c/x, onde c é a distância focal (distância entre o centro da elipse e um dos focos) e x o semieixo maior.

Partamos definindo dois ângulos na projeção em PJKW:



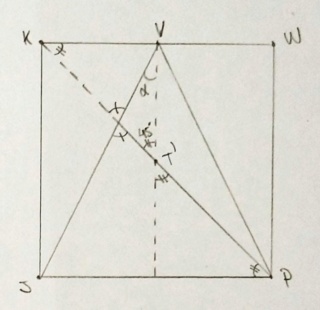
Defini o ângulo (JVP) como α e o ângulo (KT'V) é igual a 45°. Nota-se que cos α = a/[VJ]. Como [VJ] = (a√5)/2, cos α = (2√5)/5. Podemos provar (e vou provar logo em seguida) que cos 45° / cos α = e.

Prova: antes de tudo, é necessário conhecer o Teorema de Dandelin aplicado às elipses. Resumidamente, esse diz que as duas esferas inscritas acima e abaixo do plano traçado no cone tangenciam a elipse em seus focos. Em imagens, seria algo assim:




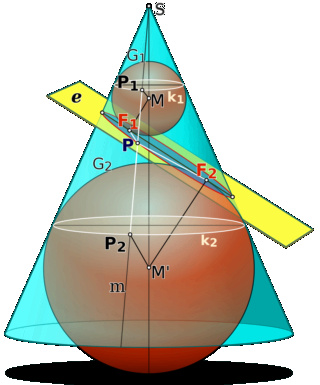
Com esse teorema em mente, façamos o seguinte desenho:



Na figura, há um plano que forma a elipse e um plano perpendicular ao cone formando um círculo no interior da esfera. Os planos se encontram formando uma reta, na qual põe-se um ponto S. A esfera em questão é uma das esferas de Dandelin e, portanto, tangencia a elipse em seu foco, denominado por F. O ponto P pertence a elipse e o ponto Q, ao circulo. O ponto R pertence ao plano do círculo. Traçam-se as retas [FP] e [PQ], de forma que essas sejam de mesma medida, já que partem de um mesmo ponto e tangenciam uma esfera. A reta [AT] é paralela ao plano do círculo e o ponto M é o centro da elipse.

A partir daí, devemos fazer a união de dois casos. `

O primeiro se trata de quando o ponto P está em A. Nesse caso, o ponto Q será o ponto B e a sua projeção será:



O segundo caso se trata de quando o ponto P está em A'. Nesse caso, Q será o ponto B' e a sua projeção será:



Caso isso não seja claro, há uma simulação no GeoGebra que mostra como variam P, Q e S em relação a elipse. Este é o link: https://www.geogebra.org/m/aNBMqngB

Unindo as duas situações, e acrescentando o ponto O, ter-se-á uma figura assim:



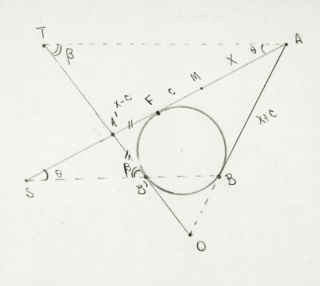
Com essa figura, podemos determinar o valor de c. Vejam que [AM] = x e [FM] = c, de modo que [AF] = x - c. Percebam, também, que B' tangencia a circunferência, de modo que [A'F] = [A'B']. Além disso, notem que [AF] = [AB] = x + c. Em posse disso, como os ângulos (BSA) e (SAT) são alternos internos, o mesmo ocorrendo para (SB'T) e (B'TA), eles são congruentes. Pela Lei dos Senos em ∆A'AT, tem-se: sen θ/[TA'] = sen β/[A'A]. Como [TA'] = [B'T] - [B'A'], [TB'] = [AB] = x + c, já que ∆TAO é isósceles e, pelo Teorema das Tangentes, [B'A'] = [A'F] = x - c, tem-se: sen θ/sen β = ([AB] - [B'A'])/[A'A] ⇒ sen θ/sen β =2c/[A'A]. Como [A'A] = 2x, vem: sen θ/sen β = 2c/2x ⇒ sen θ/sen β = c/x = e.

Isso nos mostra algo, mas não especificamente o que queríamos. Para encontrarmos a relação entre cossenos, peguemos ∆A'B'S e tracemos uma altura relativa a [SB'], teremos: 



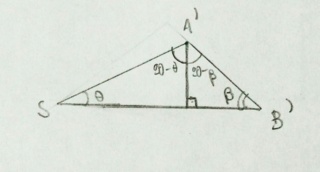
Como sen θ = cos (90º - θ) e sen β = cos (90º - β), pode-se mostrar, facilmente, que (90º - θ) e (90º - β) correspondem, respectivamente, aos ângulos 45° e α determinados no início da resolução. Acredito que não há necessidade de ilustrar: basta notar que (90º - β) é alterno interno ao ângulo formado com a altura do cone e (90º - θ) é o suplemento do ângulo formado entre os planos da elipse e do círculo.

A partir daí, as coisas se tornam mais simples. Sendo e = c/x = cos 45º/cos α. Lembrando-se que, em uma elipse, x² = y² + c², vê-se que c = √(x² - y²). Substituindo essa informação e os valores encontrados, tem-se que √(x² - y²)/x = √10/4. Desenvolvendo essa equação, conclui-se que y = (a√3)/6.

Daí, basta seguir a mesma ideia aplicada ao final da primeira solução.




Deu baita trabalho escrever isso tudo, mas queria deixar registrado aqui. Desculpe se algumas imagens não são muito claras, acabei desenhando tudo na mão mesmo e as fotos não ficam muito boas, mesmo scaneadas. Aos que chegaram ao final, parabéns kkkkkkkkkkk. Se notarem algum erro durante o desenvolvimento, avisem-me. Como há muita coisa pra escrever, às vezes algo passa despercebido. Obrigado, novamente, Gio. Lembrar do Dandelin foi fundamental.