cilindro inscrito num cone

por **boris benjamim de paula** Sáb 24 Jul 2010, 23:45

EM um cone cuja geratriz g forma com o plano da base um ângulo $\alpha$ , inscrevemos um prisma regular quadrangular; sendo as arestas laterais do prisma congruentes , determine a superficie total do prisma.

$resposta: 6(\frac{\sqrt{2lsen\alpha }}{\sqrt{2+tg\alpha }})$

por **adriano tavares** Seg 08 Nov 2010, 01:32

Olá,boris benjamim de paula.

Tem alguma coisa errada nesse gabarito,pois como são dados os valores de alpha e a geratriz g, a área do prisma que no caso em questão é um cubo deve ser em função de ambos.

Vou postar minha resolução que acredito está correta.

cilindro inscrito num cone Cuboinscritoemumcone

cilindro inscrito num cone Cuboinscritoemumcone

$ED=2r$

$BC=2R$

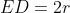
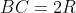
Podemos olhar a face superior do cubo se fosse um quadrado inscrito em uma circunferência, então pela geometria plana teremos:

$l=r\sqrt{2}\Rightarrow r=\frac{l\sqrt{2}}{2}\Rightarrow 2r=l\sqrt{2}$

Note que os triângulos AED e ABC são semelhantes, logo teremos:

$\frac{l\sqrt{2}}{2R}=\frac{h-l}{h}\Rightarrow lh\sqrt{2}=2Rh-2Rl\Rightarrow l=\frac{2Rh}{h\sqrt{2}+2R}$

Podemos expressar h e R em função de $\alpha$

$h=gsen\alpha$

$R=gcos\alpha$

Substituindo os valores de R e h teremos:

$l=\frac{2gsen\alpha.gcos\alpha}{\sqrt{2}gsen\alpha+2gcos\alpha}$

Da trigonometria sabemos que $2sen\alpha.cos\alpha=sen(2\alpha)$ .Substituindo teremos:

$l=\frac{gsen(2\alpha)}{\sqrt{2}sen\alpha+2cos\alpha}\Rightarrow l^2=\frac{g^2sen^2(2\alpha)}{2sen^2\alpha+2.\sqrt{2}sen\alpha.2cos\alpha+2cos^2\alpha+2cos^2\alpha}$

$l^2=\frac{g^2sen^2(2\alpha)}{2(sen^2\alpha+cos^2\alpha)+2\sqrt{2}(2sen\alpha.cos\alpha)+2cos^2\alpha}$

$l^2=\frac{g^2sen^2(2\alpha)}{2+2\sqrt{2}sen(2\alpha)+2cos^2\alpha}\Rightarrow l^2=\frac{g^2sen^2(2\alpha)}{2(1+\sqrt{2}sen(2\alpha)+cos^2\alpha)}$

$A_p=6l^2=6\frac{g^2sen^2(2\alpha)}{2(1+\sqrt{2}sen(2\alpha)+cos^2\alpha)}\Rightarrow A_p=\frac{3g^2sen^2(2\alpha)}{1+\sqrt{2}sen(2\alpha)+cos^2\alpha}$

por **Euclides** Seg 08 Nov 2010, 18:17

Tudo indica que a solução dada pelo Adriano está correta. Certamente a abordagem escolhida pode levar a expressões diferentes. Fiz uma outra abordagem e a expressão a que cheguei, apesar de mais simples e parecida com a resposta do gabarito, também é diferente:

cilindro inscrito num cone Trery

por spawnftw Sex 21 Mar 2014, 05:54

como se sabe que o prisma nesse caso é um cubo?

por Schulz Qua 21 Jan 2015, 16:36

+
+

Olá forumeiros, boa tarde!

O problema descrito abaixo pelo Boris e tentativamente resolvido pelo Euclides está me deixando "careca"!!!
Tenho a mesma dúvida colocada por por spawnftw em Sex Mar 21 2014, 04:54, isto é, o enunciado fala-se de um prisma regular quadrangular e se informa pleonasticamente que as arestas laterais do prisma são congruentes ...e daí se conclui que o prisma em questão é um cubo???

Alguém por aí já confrontou esta questão e talvez a resolveu???

Gratos Schulz

+
+