Valor mínimo para imagem de retângulo

1. PQRS é um retângulo de vértices P (-4, 0), Q (4, a) R (6,0) e S. Q encontra-se no 1° quadrante.


(i) Retângulo PQRS sofre a transformação (x, y)  (x+k, y+l ) onde k e l são números.

Começando

Coeficiente angular da reta PQ ---> m = (a - 0)/([2 - (-4)] ---> m = a/8

Equação da reta PQ ---> y - 0 = (a/.(x + 4) ---> y = (a/.x + 1/2 ---> I

Coeficiente angular da reta QR ---> m = - 8/a

Depois complete

Equação da reta PQ ---> y - 0 = (- 8/a).(x - 6) ---> y = (- 8/a).x + 48/a ---> II

Retas se cruzam em Q(4, a) ---> xQ = 4 ---> I = II ---> calcule o valor de a

Determine, de modo similar as coordenadas de S ---> S(xS, yS)

Fica entendido que a transformação referida no enunciado é uma homotetia de translação de grau 1, ou seja, há mudança da posição do retângulo por translação mas não há alteração das suas dimensões.



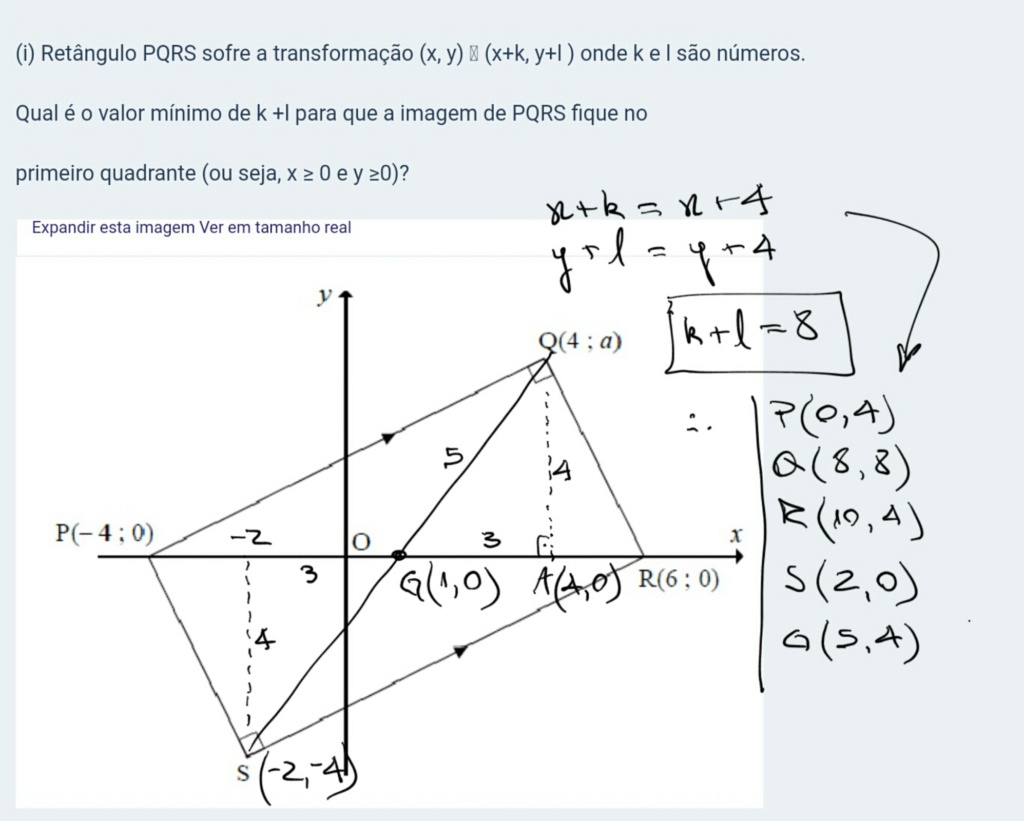
explicando o desenho
As diagonias de um retângulo cortam-se ao meio no ponto que é o baricentro da figura, portanto G (1, 0)
e meia diagonal tem medida 5.
Aprojeção de Q sobre as abscissas é o ponto A (4, 0). Portanto o triângulo QAG é um pitagórico famoso e já sabemos que o cateto QA=4, logo Q (4, 4).
Fazendo a projeção de S sobre o eixo x, por simetria ao ponto G e triângulo QAG temos que S (-2, -4).

P é o ponto extremo negativo horizontal; para jogá-lo ao primeiro quadrante precisamos pelo menos zerar sua abscissa somando 4 unidades ----> k = 4
Idem para o ponto S que é extremo negativo vertical; portanto precisamos acrescentar 4 unidades a sua ordenada ---> L = 4