Sólido de revolução
2 participantes
Página 1 de 1
 Sólido de revolução
Sólido de revolução
(Matemática - Gelson Iezzi) Os catetos de um triângulo retângulo medem 3 cm e 4 cm. Determine o volume do sólido gerado pela rotação do triângulo, usando como eixo a hipotenusa.
Resposta: 9,6 ∏ cm3
Resposta: 9,6 ∏ cm3
- DÚVIDA:
Que tipo de sólido seria formado?
 Re: Sólido de revolução
Re: Sólido de revolução
Ao girar-se um triângulo por um dos catetos, forma-se um cone. Como o eixo está na hipotenusa, podemos dividir o triângulo em dois triângulos retângulos menores, de hipotenusas iguais aos catetos do triângulo original.
Dessa forma, haverá a formação de 2 cones de mesma área da base, porém alturas diferentes.
Vtotal = Vcone1 + Vcone2
Vtotal = Abase.h1/3 + Abase.h2/3
Vtotal = Abase(h1 + h2)/3
A área da base é a área da circunferência, cujo raio é igual à distância entre o vértice que contém o ângulo reto e o eixo de rotação(hipotenusa).
r*5 = 3*4 (relação métrica)
r = 2,4 cm
Abase = πr²
Abase = 5,76π cm²
Perceba que a soma das alturas dos cones é igual à própria hipotenusa do triângulo original, que é igual a 5 cm
Vtotal = Abase(h1 + h2)/3
Vtotal = 5,76π*5/3
Vtotal = 9,6π cm³
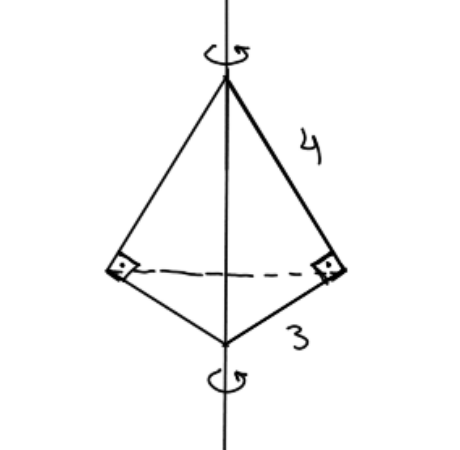
Dessa forma, haverá a formação de 2 cones de mesma área da base, porém alturas diferentes.
Vtotal = Vcone1 + Vcone2
Vtotal = Abase.h1/3 + Abase.h2/3
Vtotal = Abase(h1 + h2)/3
A área da base é a área da circunferência, cujo raio é igual à distância entre o vértice que contém o ângulo reto e o eixo de rotação(hipotenusa).
r*5 = 3*4 (relação métrica)
r = 2,4 cm
Abase = πr²
Abase = 5,76π cm²
Perceba que a soma das alturas dos cones é igual à própria hipotenusa do triângulo original, que é igual a 5 cm
Vtotal = Abase(h1 + h2)/3
Vtotal = 5,76π*5/3
Vtotal = 9,6π cm³


Renan Almeida- Matador

- Mensagens : 318
Data de inscrição : 11/08/2017
Idade : 22
Localização : Ipatinga MG Brasil
claralirasll gosta desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» Sólido de Revolução
» sólido de revolução Puc
» Sólido de revolução
» sólido de revolução Puc
» Sólido de Revolução
» sólido de revolução Puc
» Sólido de revolução
» sólido de revolução Puc
» Sólido de Revolução
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













