Fração Infinita

por castelo_hsi Seg 06 Dez 2021, 21:12

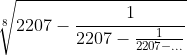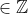Colocando-se $Fração Infinita Gif.latex?%5Csqrt%5B8%5D%7B2207-%5Cfrac%7B1%7D%7B2207-%5Cfrac%7B1%7D%7B2207-..$ sob a forma $Fração Infinita Gif$ onde a, b, c, d $Fração Infinita Gif$ o valor de a + b + c + d é igual a:

a) 10
b) 11
c) 12
d) 13
e) 14

*Questão retirada do livro do Gandhi, não tenho gabarito...

por **Giovana Martins** Dom 19 Dez 2021, 14:22

Você conseguiu chegar em algo? Achei a questão legal e fiz um esboço aqui e cheguei nisso apenas, mas não avancei muito.

[latex]\\\mathrm{x=\sqrt[8]{\mathrm{2207-\frac{1}{2207-\frac{1}{2207-...}}}}\to x^8=2207-\frac{1}{2207-\frac{1}{2207-...}}\to x^8=2207-\frac{1}{x^8}}\\\\\mathrm{(x^{8})^2-2207x^8+1=0\to (x_1,x_2)=\left ( \sqrt[8]{\frac{2}{2207+987\sqrt{5}}},\sqrt[8]{\frac{2207+987\sqrt{5}}{2}} \right )}[/latex]

por castelo_hsi Dom 19 Dez 2021, 15:00

Saudações, Giovana Martins.

Consegui resolver mas esqueci de postar... Embarassed

Resolução:

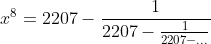
$Fração Infinita Gif.latex?x%5E%7B8%7D%3D2207-%5Cfrac%7B1%7D%7B2207-%5Cfrac%7B1%7D%7B2207-..$

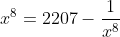
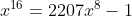
$Fração Infinita Gif$

$Fração Infinita Gif$

$Fração Infinita Gif$ ----> (I)

Fatorando essa equação, teremos:

$Fração Infinita Gif$

Para achar k:

$Fração Infinita Gif$

$Fração Infinita Gif$ ----> (II)

Logo, observe que como (II) é igual a (I), podemos descobrir o valor de k:

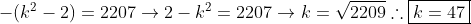
$Fração Infinita Gif$

Logo, a nossa expressão fatorada será:

$Fração Infinita Gif$

Fatorando o termo $Fração Infinita Gif$ , usando o mesmo processo, encontraremos:

$Fração Infinita Gif$

Fatorando o termo $Fração Infinita Gif$ , usando o mesmo processo, teremos:

$Fração Infinita Gif$

Ao analisarmos os termos, encontramos que o único termo que quando igualado a zero possui solução no campo dos reais é o seguinte:

$Fração Infinita Gif$

$Fração Infinita Gif$

Portanto:

$Fração Infinita Gif$

$Fração Infinita Gif$

por **Giovana Martins** Dom 19 Dez 2021, 15:57

Bem bacana a resolução! Muito obrigada!

por joaoZacharias Dom 19 Dez 2021, 16:56

Opa, eu sei que o problema já foi resolvido, mas eu achei ele muito interessante, então eu vim trazer mais uma ideia para a resolução. Usei uma técnica que é geralmente aplicada na resolução de polinômios recíprocos. Inicialmente temos:

[latex]x^8 = 2207 - \frac{1}{x^8} \implies x^8 + \frac{1}{x^8} = 2207[/latex]

Notemos a propriedade:

[latex](x^{n} + \frac{1}{x^{n}})^2 = x^{2n} + 2\frac{x^{n}}{x^{n}} + \frac{1}{x^{2n}} \implies x^{2n} + \frac{1}{x^{2n}} =(x^{n} + \frac{1}{x^{n}})^2 -2 [/latex]

Assim podemos firmar as seguinte igualdades:

[latex] x^{8} + \frac{1}{x^{8}} = (x^{4} + \frac{1}{x^{4}} )^2 -2 = ((x^{2} + \frac{1}{x^{2}} )^2 -2)^2 -2 = (((x + \frac{1}{x})^2 -2 )^2 -2)^2 -2

(((x + \frac{1}{x})^2 -2 )^2 -2)^2 = 2209 \implies ((x + \frac{1}{x})^2 -2 )^2 = 2 \pm47
[/latex]

Como temos um termo ao quadrado na igualdade a unica solucao real é:

[latex] ((x + \frac{1}{x})^2 -2 )^2 = 49 \implies (x + \frac{1}{x})^2 =2 \pm 7
[/latex]

Procedendo analogamente concluímos que:

[latex] (x + \frac{1}{x})^2 = 9 \implies (x + \frac{1}{x}) = \pm 3 \implies x^2 \pm 3\cdot x +1 =0 , \text{ } x\neq 0
[/latex]

Como o ∆ das duas equações quadráticas é igual a 5 (>0), a raiz procurada deve estar em uma delas.