Sistema Lineares
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Sistema Lineares
Sistema Lineares
Uma solução do sistema linear 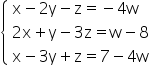 de variáveis x, y e z, para algum w real é
de variáveis x, y e z, para algum w real é
A
(4, 5, 6)
B
(4, 6, 5)
C
(5, 4, 6)
D
(5, 6, 4)
E
(6, 4, 5)
Última edição por Tsuki Mikan em Qui 25 Nov 2021, 12:29, editado 1 vez(es)

Tsuki Mikan- Jedi

- Mensagens : 287
Data de inscrição : 30/05/2021
 Re: Sistema Lineares
Re: Sistema Lineares
Como o problema quer só os valores de x, y, z vamos tentar tirar o w da jogada. Eu vou fazer por método de adição, mas o de substituição também é cabível.
[latex]-1 \cdot (x-2y -z) + (x - 3y +z) = -1 \cdot (-4w) + (7-4w) \implies 2z - y = 7 \\
4\cdot (2x + y - 3z) + (x -2y - z) = 4 \cdot ( w -8 ) + (-4w) \implies 9x + 2y - 13z = -32 \\
4\cdot (2x + y - 3z) + (x - 3y +z) = 4 \cdot ( w -8 ) + (7-4w) \implies 9x+ y - 11z = -25 [/latex]
Resolver esse novo sistema de três variáveis e três equações pelo método de sua preferência vai, eventualmente, levar a resposta. Entretanto como a questão é alternativa, para economizar tempo, basta notar que a (a) é a única resposta listada que satisfaz as relações entre y e z propostas pela equação 2z - y = 7.
[latex]-1 \cdot (x-2y -z) + (x - 3y +z) = -1 \cdot (-4w) + (7-4w) \implies 2z - y = 7 \\
4\cdot (2x + y - 3z) + (x -2y - z) = 4 \cdot ( w -8 ) + (-4w) \implies 9x + 2y - 13z = -32 \\
4\cdot (2x + y - 3z) + (x - 3y +z) = 4 \cdot ( w -8 ) + (7-4w) \implies 9x+ y - 11z = -25 [/latex]
Resolver esse novo sistema de três variáveis e três equações pelo método de sua preferência vai, eventualmente, levar a resposta. Entretanto como a questão é alternativa, para economizar tempo, basta notar que a (a) é a única resposta listada que satisfaz as relações entre y e z propostas pela equação 2z - y = 7.

joaoZacharias- Recebeu o sabre de luz

- Mensagens : 134
Data de inscrição : 18/03/2020
Localização : Campinas - SP, BR
 Re: Sistema Lineares
Re: Sistema Lineares
João, obrigada pela resolução da questão

Tsuki Mikan- Jedi

- Mensagens : 287
Data de inscrição : 30/05/2021
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













