INEQUAÇÂO MODULAR- ESCOLA NAVAL

por Jvictors021 Qua 13 Out 2021, 18:50

Qual o conjunto solução da inequação 3|x-1| + x > |1-x| é:

Gab: (-∞, +∞)

Bati muito a cabeça com essa questão, se puderem explica-la fico grato

por **qedpetrich** Qua 13 Out 2021, 19:20

Olá Jvictors;

Aplicando a definição modular para x-1:

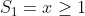
$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png.latex?%7Cx-1%7C%20%3D%20%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%20x-1%2C%20%5C%20se%20%5C%20x%20%5Cgeq%201%20%26%20%5C%5C%20-x+1%2C%20%5C%20se%20%5C%20x%20%3C%201%20%26%20%5Cend%7Bmatrix%7D%5Cright$

Aplicando a definição modular para -x+1:

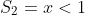
$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png.latex?%7C-x+1%7C%20%3D%20%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%20x-1%2C%20%5C%20se%20%5C%20x%20%5Cgeq%201%20%26%20%5C%5C%20-x+1%2C%20%5C%20se%20%5C%20x%20%3C%201%20%26%20%5Cend%7Bmatrix%7D%5Cright$

Se x ≥ 1, logo:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Como x ≥ 1, logo, nossa solução é a própria condição, temos:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Se x < 1, logo:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Como x < 1, logo, nossa solução é a própria condição, temos:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

A solução da inequação modular é dada pela união entre S1 e S2:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Espero ter ajudado!

por Jvictors021 Ter 19 Out 2021, 05:04

qedpetrich escreveu:Olá Jvictors;

Aplicando a definição modular para x-1:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png.latex?%7Cx-1%7C%20%3D%20%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%20x-1%2C%20%5C%20se%20%5C%20x%20%5Cgeq%201%20%26%20%5C%5C%20-x+1%2C%20%5C%20se%20%5C%20x%20%3C%201%20%26%20%5Cend%7Bmatrix%7D%5Cright$

Aplicando a definição modular para -x+1:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png.latex?%7C-x+1%7C%20%3D%20%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%20x-1%2C%20%5C%20se%20%5C%20x%20%5Cgeq%201%20%26%20%5C%5C%20-x+1%2C%20%5C%20se%20%5C%20x%20%3C%201%20%26%20%5Cend%7Bmatrix%7D%5Cright$

Se x ≥ 1, logo:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Como x ≥ 1, logo, nossa solução é a própria condição, temos:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Se x < 1, logo:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Como x < 1, logo, nossa solução é a própria condição, temos:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

A solução da inequação modular é dada pela união entre S1 e S2:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Espero ter ajudado!

Muito bom qedpetrich, mas caso os 2 módulos tivessem restrições diferentes como eu prosseguiria ??

por exemplo: 3|x-2| + x > |1-x|

|x - 2| = (x-2) se x ≥ 2
|x - 2| = (-x+2) se x < 2
e
|1-x| = (1-x) se x ≤ 1
|1-x| = (-1+x) se x > 1

por **Giovana Martins** Ter 19 Out 2021, 09:30

Um outro jeito via resolução gráfica: sejam f(x)=3|x-1|+x e g(x)=|1-x|. Plotando ambos os gráficos:

INEQUAÇÂO MODULAR- ESCOLA NAVAL Oie_t100

Note que para todo x real tem-se f(x) > g(x). Por exemplo, para x=±2 (retas tracejadas em vermelho), tem-se f(x) > g(x). Pela conformação gráfica de cada curva nota-se que o mesmo ocorre para os demais valores de x.

Nota: se houver dúvidas quanto ao esboço de cada curva ou sobre qualquer outra coisa, me avise.

por Jvictors021 Ter 19 Out 2021, 10:02

Giovana Martins escreveu:
Um outro jeito via resolução gráfica: sejam f(x)=3|x-1|+x e g(x)=|1-x|. Plotando ambos os gráficos:

Note que para todo x real tem-se f(x) > g(x). Por exemplo, para x=±2 (retas tracejadas em vermelho), tem-se f(x) > g(x). Pela conformação gráfica de cada curva nota-se que o mesmo ocorre para os demais valores de x.

Nota: se houver dúvidas quanto ao esboço de cada curva ou sobre qualquer outra coisa, me avise.

Muito bom mesmo giovana.... faz todo o sentido o problema era eu ter pensado nisso na resolução hahahaha!! Parabéns, vc é fera

por **Giovana Martins** Ter 19 Out 2021, 10:26

Ah, até alguém me ensinar a resolver questões dessa forma eu também não sabia muito bem como proceder Smile

. Bom que agora você tem duas alternativas de resolução para questões assim. Se você se deparar com outra questão assim, basta resolvê-la de modo semelhante. A propósito, se você ainda não conhece o Geogebra, sugiro que você o use, especialmente em questões sobre funções. Esse software ajuda demais nos estudos.

por **qedpetrich** Ter 19 Out 2021, 13:39

Jvictors021 escreveu:Muito bom qedpetrich, mas caso os 2 módulos tivessem restrições diferentes como eu prosseguiria ??

por exemplo: 3|x-2| + x > |1-x|

|x - 2| = (x-2) se x ≥ 2
|x - 2| = (-x+2) se x < 2
e
|1-x| = (1-x) se x ≤ 1
|1-x| = (-1+x) se x > 1

Aplicou corretamente as definições modulares, prossegue-se desta forma:

Se x ≥ 2, logo:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Mas como condição x ≥ 2, portanto:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Se 1 < x < 2, logo:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Mas como condição 1 < x < 2, portanto:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Se x ≤ 1, logo:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Mas como condição x ≤ 1, portanto:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Nossa solução para a inequação modular como um todo é dada pela união de S₁ U S₂ U S₃:

$INEQUAÇÂO MODULAR- ESCOLA NAVAL Png$

Nesses casos é mais inteligente recorrer as soluções gráficas como a Giovana Martins explorou. É tanta operação e restrição que fica fácil acabar negligenciando alguma parte. Pegue a dica da colega e desfrute do Geogebra, realmente é uma ferramenta muito útil que salva demaisss, vai ajudar bastante para seu aprendizado. De qualquer forma espero que tenha clareado sua mente!