UFMG, Plano cartesiano

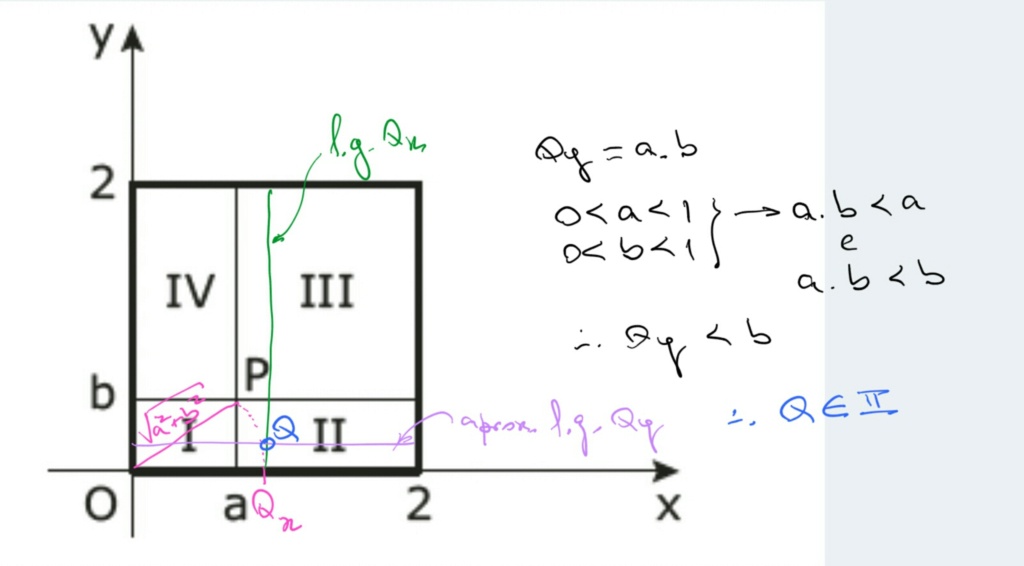
Seja P(a, b) um ponto no plano cartesiano, tal que 0 < a < 1 e 0 < b < 1. As retas paralelas aos eixos
coordenados que passam por P dividem o quadrado de vértices (0, 0), (2, 0), (0, 2) e (2, 2) nas regiões I, II, III e IV, como mostrado nesta figura:






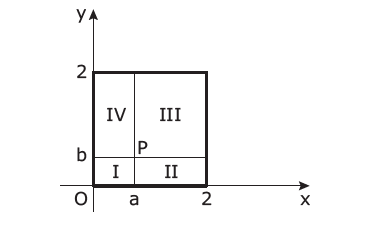
Considere o ponto Q = ([latex]Q = \sqrt{a^2+b^2}[/latex],ab)

Então, é CORRETO afirmar que o ponto Q está na região

A) I. B) II. C) III.  D) IV.


Gabarito B

... como mostrado nesta ?????

Parece que o enunciado está incompleto. Será que faltou uma figura?
Por favor, verifique e complemente.

Realmente faltou a imagem, obrigado por avisar.

Eu fiquei em dúvida entre a ou b, não consegui provar que o valor de x para ponto Q é está entre I ou II.

ab<1, pois multiplicar dois números menos que 1, dá um resultado menor que 1, logo o valor y para o ponto que é menor que 1.

Q(√(a² + b²) ; a.b)

xQ = √(a² + b²) ---> xQ pode ser:

1) xQ < 1, por exemplo para a = 0,5 e b = 0,4
2) xQ = 1, por exemplo para a = 0,8 e b = 0,6
3) xQ > 1, por exemplo para x = 0,7 e b = 0,8

yQ = a.b ---> Como a < 1 e b < 1 ---> a.b < 1 ---> yQ < 1 (só pode ser I ou II)

Tente completar.

Então Elcio, cheguei nesse mesmo resultado, eu não estou conseguindo provar que o valor de xQ é maior que 1 ou ao menos maior que "a" para cair no retângulo II.

Bruno

veja se a figura abaixo é suficiente para o entendimento. Usei o conceito de lugar geométrico (l.g.) das coordenadas do ponto Q.

lembrando que as regiões I, ... , IV variam conforme a posição do ponto P.

Fico sem graça de dizer, mas não entendi. Pode dar mais detalhe explicando esta imagem, se possível !?

Sinto que sua explicação tem a ver com isso aqui:



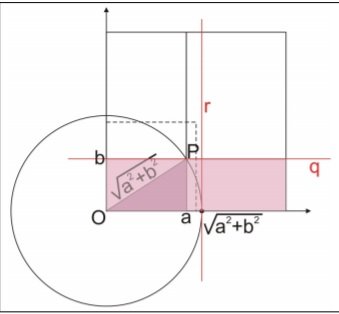
Essa imagem eu tirei do site tutorbrasil no qual um membro do fórum postou, a explicação no qual eu não entendi (e por isso postei aqui no fórum) foi essa:

Como ab é um número positivo ao mesmo tempo menor que a e que b, pela análise da .figura abaixo chegamos à conclusão de que a abscissa[latex]\sqrt{a^2+b^2}[/latex]  do ponto Q está sobre a reta r e que a sua ordenada ab está no interior da região destacada .

É isso aí mesmo, Bruno. Esse desenho que você trouxe é similar ao meu.

A abscissa de Q tem mesmo valor do segmento OP, que obviamente é maior que a, conforme mostrado no desenho. Portanto o ponto Q está sobre o segmento de reta que fica dentro do quadrado -- este é um lugar geométrico de Qx.

A ordenada de Q é a.b, que por sua vez é sempre menor que a e menor que b, pois ambos são positivos e menores do que 1. Portanto o outro lugar geométrico de Q é a região destacada -- com a ressalva de que essa região não chega na ordenada b. No meu desenho tracei uma linha hipotética para esse Qy.

O ponto Q tem que atender às duas condições (dadas pelos lugares geométricos de Qx e Qy), logo ele fica na interseção delas.

Obrigado Medeiros, entendido!