Geometria e sinuca

Uma mesa de bilhar possui 6 buracos nos quais caem as bolas que estão em jogo. Em determinada mesa, a razão
entre a medida da largura e do comprimento, nessa ordem, é 5/7
. Uma bola estava posicionada bem próxima a um
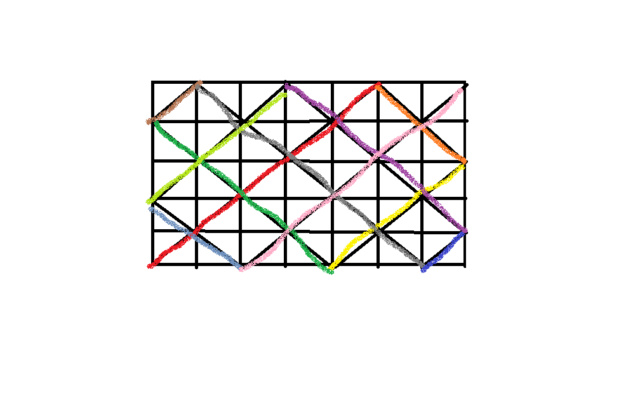
buraco e um jogador bateu nela com o taco de forma que o prolongamento desse último seja a bissetriz do ângulo reto
do canto da mesa, conforme mostra a figura 1.
Considere que quando a bola bate na lateral da mesa, ela é rebatida com o mesmo ângulo que incidiu nessa lateral
(ver figura 2).
Admitindo que a bola foi batida com força suficiente para cair em um buraco, então ela bateu nas laterais.

Gabarito C, minha dúvida está em se existe uma forma mais rápida de fazer essa questão além de traçar  cada caminho?

Olá

desconheço forma mais rápida, acho traçar o caminho o melhor método. Por sorte o ângulo inicial é 45°, assim todas as reflexões são nesse mesmo ângulo.